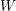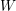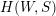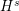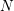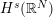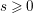Contents
Article
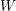 $W$ -GRAPHS AND GYOJA’S
$W$ -GRAPHS AND GYOJA’S 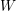 $W$ -GRAPH ALGEBRA
$W$ -GRAPH ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1-43
-
- Article
-
- You have access
- HTML
- Export citation
NON-REGULARITY IN HÖLDER AND SOBOLEV SPACES OF SOLUTIONS TO THE SEMILINEAR HEAT AND SCHRÖDINGER EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2016, pp. 44-70
-
- Article
-
- You have access
- HTML
- Export citation
A RECOLLEMENT APPROACH TO GEIGLE–LENZING WEIGHTED PROJECTIVE VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2016, pp. 71-105
-
- Article
-
- You have access
- HTML
- Export citation
SALLY MODULES AND REDUCTION NUMBERS OF IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2016, pp. 106-126
-
- Article
-
- You have access
- HTML
- Export citation
BOUNDARY PARAMETRIZATION AND THE TOPOLOGY OF TILES
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 127-164
-
- Article
-
- You have access
- HTML
- Export citation
CANONICAL AND
 $n$ -CANONICAL MODULES OF A NOETHERIAN ALGEBRA
$n$ -CANONICAL MODULES OF A NOETHERIAN ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2016, pp. 165-203
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
NMJ volume 226 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 May 2017, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
NMJ volume 226 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 May 2017, pp. b1-b5
-
- Article
-
- You have access
- Export citation