Hostname: page-component-cb9f654ff-5kfdg Total loading time: 0 Render date: 2025-08-29T08:34:08.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Units and Cyclotomic Units in Zp -Extensions

Published online by Cambridge University Press:  22 January 2016

Jae Moon Kim
Jae Moon Kim*
Affiliation:
Department of Mathematics, Inha University, Inchon, Korea (e-mail) jmkim@munhak.inha.ac.kr
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p be an odd prime and d be a positive integer prime to p such that d ≢ 2 mod 4. For technical reasons, we also assume that 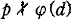. For each integer n ≥ 1, we choose a primitive nth root ζn of 1 so that 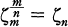whenever n | m. Let 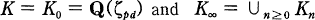be its cyclotomic Zp-extension, where 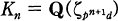is the nth layer of this extension. For n ≤ 1, we denote the Galois group Ga\(Kn/K0 ) by Gn , the unit group of the ring of integers of Kn by En , and the group of cyclotomic units of Kn by Cn . For the definition and basic properties of cyclotomic units such as the index theorem, we refer [6] and [7]. In this paper we examine the injectivity of the homomorphism 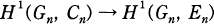between the first cohomology groups induced by the inclusion Cn → En .

Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 140 , December 1995 , pp. 101 - 116
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[ 1 ] Ennola, V., On relations between cyclotomic units, J. Number Theory, 4 (1972), 236–247.Google Scholar
[2] Gold, R., Kim, J. M., Bases for cyclotomic units, Compositio Math., 71 (1989), 13–28.Google Scholar
[ 3 ] Iwasawa, K., On Cohomology groups of units for Zp-extensions, Amer. J. Math., 105 No.1 (1983), 189–200.Google Scholar
[4] Kim, J. M., Cohomology groups of cyclotomic units, J. Algebra, 152, no.2 (1992), 514–519.Google Scholar
[ 5 ] Kim, J. M., Coates-Wiles series and Mirimanoff’s polynomial, J. Number Theory, 54, No.2 (1995), 173–179.Google Scholar
[ 6 ] Sinnott, W., On the Stickelberger ideal and the circular units of a cyclotomic field, Ann. of Math., (2) 108 (1978), 107–134.CrossRefGoogle Scholar
[ 7 ] Washington, L., Introduction to Cyclotomic Fields, G. T. M., Springer-Verlag, New York, 1980.Google Scholar