Article contents
The topology of an open manifold with radial curvature bounded from below by a model surface with finite total curvature and examples of model surfaces
Published online by Cambridge University Press: 11 January 2016
Abstract
We construct distinctive surfaces of revolution with finite total curvature whose Gauss curvatures are not bounded. Such a surface of revolution is employed as a reference surface of comparison theorems in radial curvature geometry. Moreover, we prove that a complete noncompact Riemannian manifold M is homeomorphic to the interior of a compact manifold with boundary if the manifold M is not less curved than a noncompact model surface 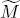 of revolution and if the total curvature of the model surface
of revolution and if the total curvature of the model surface 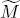 is finite and less than 2π. By the first result mentioned above, the second result covers a much wider class of manifolds than that of complete noncompact Riemannian manifolds whose sectional curvatures are bounded from below by a constant.
is finite and less than 2π. By the first result mentioned above, the second result covers a much wider class of manifolds than that of complete noncompact Riemannian manifolds whose sectional curvatures are bounded from below by a constant.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 2013
References
- 3
- Cited by

