Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Duke, William
and
Schulze-Pillot, Rainer
1990.
Representation of integers by positive ternary quadratic forms and equidistribution of lattice points on ellipsoids.
Inventiones Mathematicae,
Vol. 99,
Issue. 1,
p.
49.
Böcherer, Siegfried
and
Schulze-Pillot, Rainer
1992.
The Dirichlet series of Koecher and Maaß and modular forms of weight 3/2.
Mathematische Zeitschrift,
Vol. 209,
Issue. 1,
p.
273.
Böcherer, Siegfried
and
Schulze‐Pillot, Rainer
1994.
Mellin Transforms of Vector Valued Theta Series Attached to Quaternion Algebras.
Mathematische Nachrichten,
Vol. 169,
Issue. 1,
p.
31.
Xu, Fei
2001.
Representation masses of spinor genera.
Duke Mathematical Journal,
Vol. 110,
Issue. 2,
Cogdell, James W.
2003.
On sums of three squares.
Journal de théorie des nombres de Bordeaux,
Vol. 15,
Issue. 1,
p.
33.
Schulze-Pillot, Rainer
2017.
Averages of Fourier coefficients of Siegel modular forms and representation of binary quadratic forms by quadratic forms in four variables.
Mathematische Annalen,
Vol. 368,
Issue. 3-4,
p.
923.
Voight, John
2023.
Kneser’s method of neighbors.
Archiv der Mathematik,
Vol. 121,
Issue. 5-6,
p.
537.

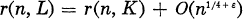 . The main tool utilized for the proof was the theory of modular forms of weight 3/2, especially Shimura’s lifting from the space of cusp forms of weight 3/2 to the space of modular forms of weight 2.
. The main tool utilized for the proof was the theory of modular forms of weight 3/2, especially Shimura’s lifting from the space of cusp forms of weight 3/2 to the space of modular forms of weight 2.