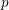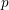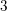1 Introduction
The position of simple modules in the stable Auslander–Reiten quiver of the group algebra
![]() $kG$
over a field
$kG$
over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
of a finite group
$p$
of a finite group
![]() $G$
of order divisible by
$G$
of order divisible by
![]() $p$
is a question that was partially investigated in the 1980s and the 1990s in a series of articles by different authors. We refer the reader in particular to [Reference Bessenrodt and Uno4, Reference Kawata20–Reference Kawata, Michler and Uno22] and the references therein. The aim of this note is to come back to the following question:
$p$
is a question that was partially investigated in the 1980s and the 1990s in a series of articles by different authors. We refer the reader in particular to [Reference Bessenrodt and Uno4, Reference Kawata20–Reference Kawata, Michler and Uno22] and the references therein. The aim of this note is to come back to the following question:
Question A. Let
![]() $B$
be a wild
$B$
be a wild
![]() $p$
-block of
$p$
-block of
![]() $kG$
. Under which conditions do all simple
$kG$
. Under which conditions do all simple
![]() $B$
-modules lie at the end of their connected components in the stable Auslander–Reiten quiver of
$B$
-modules lie at the end of their connected components in the stable Auslander–Reiten quiver of
![]() $kG$
?
$kG$
?
A main reason of interest in this question lies in the fact that a simple
![]() $kG$
-module lies at the end of its component if and only if the heart of its projective cover is indecomposable.
$kG$
-module lies at the end of its component if and only if the heart of its projective cover is indecomposable.
In this article, we focus attention on the case in which the principal block
![]() $B_{0}(kG)$
is of wild representation type with abelian defect groups and the prime
$B_{0}(kG)$
is of wild representation type with abelian defect groups and the prime
![]() $p$
is odd. We recall that a
$p$
is odd. We recall that a
![]() $p$
-block is of wild representation type if and only if its defect groups are neither cyclic, nor dihedral, nor semidihedral, nor generalized quaternion (see [Reference Humphreys18, §8.9 Theorem]). Thus, when
$p$
-block is of wild representation type if and only if its defect groups are neither cyclic, nor dihedral, nor semidihedral, nor generalized quaternion (see [Reference Humphreys18, §8.9 Theorem]). Thus, when
![]() $p$
is odd, this amounts to requiring that the
$p$
is odd, this amounts to requiring that the
![]() $p$
-rank of
$p$
-rank of
![]() $G$
is at least
$G$
is at least
![]() $2$
. Question A in the case that
$2$
. Question A in the case that
![]() $p=2$
was treated by Kawata et al. in [Reference Kawata, Michler and Uno21, Theorem 5]. We aim at extending their results and part of their methods to arbitrary primes. Further, we note that the cases when
$p=2$
was treated by Kawata et al. in [Reference Kawata, Michler and Uno21, Theorem 5]. We aim at extending their results and part of their methods to arbitrary primes. Further, we note that the cases when
![]() $B_{0}(kG)$
is of finite or tame representation type are well understood. In the former case, the distance of a simple module to the rim of its connected component (which is a tube of shape
$B_{0}(kG)$
is of finite or tame representation type are well understood. In the former case, the distance of a simple module to the rim of its connected component (which is a tube of shape
![]() $(\mathbb{Z}/\!e\mathbb{Z})A_{m}$
) is a function of its position in the Brauer tree of the block, while in the latter case the position of the simple modules in their connected components is given by Erdmann’s work on tame blocks [Reference Erdmann10].
$(\mathbb{Z}/\!e\mathbb{Z})A_{m}$
) is a function of its position in the Brauer tree of the block, while in the latter case the position of the simple modules in their connected components is given by Erdmann’s work on tame blocks [Reference Erdmann10].
Assuming the field
![]() $k$
is algebraically closed we prove the following results:
$k$
is algebraically closed we prove the following results:
Theorem B. Let
![]() $G$
be a finite group and
$G$
be a finite group and
![]() $N\unlhd G$
a normal subgroup such that
$N\unlhd G$
a normal subgroup such that
![]() $G/N$
is solvable of
$G/N$
is solvable of
![]() $p^{\prime }$
-order. Let
$p^{\prime }$
-order. Let
![]() $B$
and
$B$
and
![]() $b$
be wild blocks of
$b$
be wild blocks of
![]() $kG$
and
$kG$
and
![]() $kN$
, respectively, such that
$kN$
, respectively, such that
![]() $1_{B}=1_{b}$
. If every simple
$1_{B}=1_{b}$
. If every simple
![]() $b$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
$b$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
![]() $kN$
, then every simple
$kN$
, then every simple
![]() $B$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
$B$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
![]() $kG$
.
$kG$
.
Theorem C. Let
![]() $p$
be an odd prime. Let
$p$
be an odd prime. Let
![]() $G$
be a finite group with noncyclic abelian Sylow
$G$
be a finite group with noncyclic abelian Sylow
![]() $p$
-subgroups and
$p$
-subgroups and
![]() $O_{p^{\prime }}(G)=1$
. Write
$O_{p^{\prime }}(G)=1$
. Write
![]() $O^{p^{\prime }}(G)=Q\times H_{1}\times \cdots \times H_{m}$
(
$O^{p^{\prime }}(G)=Q\times H_{1}\times \cdots \times H_{m}$
(
![]() $m\geqslant 0$
), where
$m\geqslant 0$
), where
![]() $Q$
is an abelian
$Q$
is an abelian
![]() $p$
-group and
$p$
-group and
![]() $H_{i}$
is a nonabelian finite simple group with nontrivial Sylow
$H_{i}$
is a nonabelian finite simple group with nontrivial Sylow
![]() $p$
-subgroups for each
$p$
-subgroups for each
![]() $1\leqslant i\leqslant m$
. Assume that one of the following conditions is satisfied:
$1\leqslant i\leqslant m$
. Assume that one of the following conditions is satisfied:
(i)
 $Q\neq 1$
; or
$Q\neq 1$
; or(ii)
 $Q=1$
and
$Q=1$
and
 $m\geqslant 2$
; or
$m\geqslant 2$
; or(iii)
 $Q=1$
,
$Q=1$
,
 $m=1$
and every simple
$m=1$
and every simple
 $B_{0}(kH_{1})$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
$B_{0}(kH_{1})$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
 $kH_{1}$
.
$kH_{1}$
.
Then every simple
![]() $B_{0}(kG)$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
$B_{0}(kG)$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
![]() $kG$
.
$kG$
.
Corollary D. Let
![]() $p$
be an odd prime. Assume that every simple
$p$
be an odd prime. Assume that every simple
![]() $B_{0}(kH)$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
$B_{0}(kH)$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
![]() $kH$
for every nonabelian finite simple group
$kH$
for every nonabelian finite simple group
![]() $H$
with noncyclic abelian Sylow
$H$
with noncyclic abelian Sylow
![]() $p$
-subgroups. Then every simple
$p$
-subgroups. Then every simple
![]() $B_{0}(kG)$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
$B_{0}(kG)$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
![]() $kG$
for any finite group
$kG$
for any finite group
![]() $G$
with noncyclic abelian Sylow
$G$
with noncyclic abelian Sylow
![]() $p$
-subgroups.
$p$
-subgroups.
We note that if
![]() $p=2$
, then the analogues of Theorem C and Corollary D were essentially proven by Kawata et al. [Reference Kawata, Michler and Uno21], although not stated in these terms. As a corollary, we also obtain the equivalent of [Reference Kawata, Michler and Uno21, Theorem 5(a)] for the prime
$p=2$
, then the analogues of Theorem C and Corollary D were essentially proven by Kawata et al. [Reference Kawata, Michler and Uno21], although not stated in these terms. As a corollary, we also obtain the equivalent of [Reference Kawata, Michler and Uno21, Theorem 5(a)] for the prime
![]() $3$
.
$3$
.
Theorem E. Assume
![]() $p=3$
. Let
$p=3$
. Let
![]() $G$
be a finite group with abelian Sylow
$G$
be a finite group with abelian Sylow
![]() $3$
-subgroups. If
$3$
-subgroups. If
![]() $B_{0}(kG)$
is a wild
$B_{0}(kG)$
is a wild
![]() $3$
-block, then every simple
$3$
-block, then every simple
![]() $B_{0}(kG)$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
$B_{0}(kG)$
-module lies at the end of its connected component in the stable Auslander–Reiten quiver of
![]() $kG$
.
$kG$
.
The paper is organized as follows: in Section 2, we set up the notation and in Section 3 we recall the state of knowledge on the subject and extend a result of Kawata’s [Reference Kawata20, Theorem 1.5] to describe more precisely the indecomposable summands of the heart of the projective cover of a simple module not lying on the rim of its component. In Section 4, we consider groups having a solvable quotient of
![]() $p^{\prime }$
-order and prove Theorem B. In Sections 5 and 6, we proceed to a reduction of Question A for principal blocks to the case of finite nonabelian simple groups and prove Theorem C and Corollary D. Finally in Section 7 we deal with the case
$p^{\prime }$
-order and prove Theorem B. In Sections 5 and 6, we proceed to a reduction of Question A for principal blocks to the case of finite nonabelian simple groups and prove Theorem C and Corollary D. Finally in Section 7 we deal with the case
![]() $p=3$
and prove Theorem E.
$p=3$
and prove Theorem E.
2 Notation and preliminaries on module and block theory
Throughout this paper, unless otherwise stated, we adopt the following notation and conventions. We assume that
![]() $k$
is an algebraically closed field of characteristic
$k$
is an algebraically closed field of characteristic
![]() $p>0$
. All groups are assumed to be finite and we let
$p>0$
. All groups are assumed to be finite and we let
![]() $G$
denote a finite group of order divisible
$G$
denote a finite group of order divisible
![]() $p$
. We let
$p$
. We let
![]() $({\mathcal{K}},{\mathcal{O}},k)$
be a splitting
$({\mathcal{K}},{\mathcal{O}},k)$
be a splitting
![]() $p$
-modular system for
$p$
-modular system for
![]() $G$
and its subgroups, namely
$G$
and its subgroups, namely
![]() ${\mathcal{O}}$
is a complete discrete vatulation ring,
${\mathcal{O}}$
is a complete discrete vatulation ring,
![]() ${\mathcal{K}}$
its quotient field of characteristic
${\mathcal{K}}$
its quotient field of characteristic
![]() $0$
,
$0$
,
![]() $k={\mathcal{O}}/J({\mathcal{O}})$
its residue field of characteristic
$k={\mathcal{O}}/J({\mathcal{O}})$
its residue field of characteristic
![]() $p$
(where
$p$
(where
![]() $J({\mathcal{O}})$
is the unique maximal ideal of
$J({\mathcal{O}})$
is the unique maximal ideal of
![]() ${\mathcal{O}}$
), and
${\mathcal{O}}$
), and
![]() ${\mathcal{K}}$
and
${\mathcal{K}}$
and
![]() $k$
are both splitting fields for all subgroups of
$k$
are both splitting fields for all subgroups of
![]() $G$
.
$G$
.
For a
![]() $p$
-block
$p$
-block
![]() $B$
, we write
$B$
, we write
![]() $1_{B}$
for the corresponding block idempotent and
$1_{B}$
for the corresponding block idempotent and
![]() $\text{IBr}(B)$
for the set of isomorphism classes of simple
$\text{IBr}(B)$
for the set of isomorphism classes of simple
![]() $kB$
-modules. Furthermore, unless otherwise specified, we assume that
$kB$
-modules. Furthermore, unless otherwise specified, we assume that
![]() $B_{0}=B_{0}(kG)$
, the principal block of
$B_{0}=B_{0}(kG)$
, the principal block of
![]() $kG$
, is wild. Thus, when the defect groups of
$kG$
, is wild. Thus, when the defect groups of
![]() $B$
are abelian, we may therefore assume that a Sylow
$B$
are abelian, we may therefore assume that a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $G$
is noncyclic, or equivalently that the
$G$
is noncyclic, or equivalently that the
![]() $p$
-rank of
$p$
-rank of
![]() $G$
is at least
$G$
is at least
![]() $2$
.
$2$
.
We write
![]() $H\leqslant G$
if
$H\leqslant G$
if
![]() $H$
is a subgroup of
$H$
is a subgroup of
![]() $G$
,
$G$
,
![]() $N\unlhd G$
if
$N\unlhd G$
if
![]() $N$
is a normal subgroup of
$N$
is a normal subgroup of
![]() $G$
,
$G$
,
![]() $O_{p^{\prime }}(G)$
for the largest
$O_{p^{\prime }}(G)$
for the largest
![]() $p^{\prime }$
-normal subgroup of
$p^{\prime }$
-normal subgroup of
![]() $G$
, and
$G$
, and
![]() $O^{p^{\prime }}(G)$
for the smallest normal subgroup of
$O^{p^{\prime }}(G)$
for the smallest normal subgroup of
![]() $G$
with
$G$
with
![]() $p^{\prime }$
-index in
$p^{\prime }$
-index in
![]() $G$
. All modules are assumed to be finitely generated right modules. We denote by
$G$
. All modules are assumed to be finitely generated right modules. We denote by
![]() $k_{G}$
the trivial
$k_{G}$
the trivial
![]() $kG$
-module. If
$kG$
-module. If
![]() $H\leqslant G$
and
$H\leqslant G$
and
![]() $X$
,
$X$
,
![]() $Y$
are
$Y$
are
![]() $kG$
- and
$kG$
- and
![]() $kH$
-modules, respectively, then we write
$kH$
-modules, respectively, then we write
![]() $X\downarrow _{H}$
for the restriction of
$X\downarrow _{H}$
for the restriction of
![]() $X$
to
$X$
to
![]() $H$
, and
$H$
, and
![]() $Y\uparrow ^{G}=Y\otimes _{kH}kG$
for the induction of
$Y\uparrow ^{G}=Y\otimes _{kH}kG$
for the induction of
![]() $Y$
from
$Y$
from
![]() $H$
to
$H$
to
![]() $G$
.
$G$
.
We let
![]() $J=J(kG)$
denote the Jacobson radical of
$J=J(kG)$
denote the Jacobson radical of
![]() $kG$
. For a
$kG$
. For a
![]() $kG$
-module
$kG$
-module
![]() $U$
, we define
$U$
, we define
![]() $J(kG)^{0}=kG$
and for any nonnegative integer
$J(kG)^{0}=kG$
and for any nonnegative integer
![]() $i\geqslant 0$
we let
$i\geqslant 0$
we let
![]() $\text{soc}^{i}(U)=\{u\in U\,|\,u\,J^{i}=\{0\}\}$
, then inductively for any
$\text{soc}^{i}(U)=\{u\in U\,|\,u\,J^{i}=\{0\}\}$
, then inductively for any
![]() $i\geqslant 1$
, we write
$i\geqslant 1$
, we write
for the
![]() $i$
th Loewy layer and the
$i$
th Loewy layer and the
![]() $i$
th socle layer of
$i$
th socle layer of
![]() $U$
, respectively. We define
$U$
, respectively. We define
![]() $\text{soc}(U)=\text{soc}^{0}(U)$
, that is called the socle of
$\text{soc}(U)=\text{soc}^{0}(U)$
, that is called the socle of
![]() $U$
(see [Reference Landrock29, Chapter I, Definition 8.1]). For an integer
$U$
(see [Reference Landrock29, Chapter I, Definition 8.1]). For an integer
![]() $n\geqslant 1$
and simple
$n\geqslant 1$
and simple
![]() $kG$
-modules
$kG$
-modules
![]() $S_{1},\ldots ,S_{n}$
(possibly
$S_{1},\ldots ,S_{n}$
(possibly
![]() $S_{i}\cong S_{j}$
for
$S_{i}\cong S_{j}$
for
![]() $i\not =j$
) we denote by
$i\not =j$
) we denote by

a uniserial
![]() $kG$
-module of Loewy length
$kG$
-module of Loewy length
![]() $n$
such that
$n$
such that
![]() $L_{i}(U)\cong S_{i}$
for every
$L_{i}(U)\cong S_{i}$
for every
![]() $1\leqslant i\leqslant n$
. We also recall that the Loewy series does not determine modules up to isomorphism. For instance if
$1\leqslant i\leqslant n$
. We also recall that the Loewy series does not determine modules up to isomorphism. For instance if
![]() $p=2$
and
$p=2$
and
![]() $G=C_{2}\times C_{2}$
, then
$G=C_{2}\times C_{2}$
, then
![]() $kG\cong k[x,y]/(x^{2},y^{2})$
as
$kG\cong k[x,y]/(x^{2},y^{2})$
as
![]() $k$
-algebras and there are obviously two nonisomorphic uniserial
$k$
-algebras and there are obviously two nonisomorphic uniserial
![]() $kG$
-modules
$kG$
-modules
![]() $U$
and
$U$
and
![]() $V$
of Loewy length
$V$
of Loewy length
![]() $2$
(
$2$
(
![]() $\dim _{k}[\text{Ext}_{kG}^{1}(k,k)]=2$
). We will use throughout the following well-known properties without further mention:
$\dim _{k}[\text{Ext}_{kG}^{1}(k,k)]=2$
). We will use throughout the following well-known properties without further mention:
Lemma 2.1. Assume
![]() $N\unlhd G$
of index prime to
$N\unlhd G$
of index prime to
![]() $p$
.
$p$
.
(a) We have
 $J=\tilde{J}\,kG=kG\,\tilde{J}$
where
$J=\tilde{J}\,kG=kG\,\tilde{J}$
where
 $\tilde{J}=J(kN)$
.
$\tilde{J}=J(kN)$
.(b) Let
 $X$
be a
$X$
be a
 $kG$
-module and
$kG$
-module and
 $Y$
a
$Y$
a
 $kN$
-module, then for any
$kN$
-module, then for any
 $i\geqslant 1$
we have and
$i\geqslant 1$
we have and $$\begin{eqnarray}L_{i}(X)\downarrow _{N}=L_{i}(X\downarrow _{N})\quad \text{and}\quad S_{i}(X)\downarrow _{N}=S_{i}(X\downarrow _{N})\end{eqnarray}$$
$$\begin{eqnarray}L_{i}(X)\downarrow _{N}=L_{i}(X\downarrow _{N})\quad \text{and}\quad S_{i}(X)\downarrow _{N}=S_{i}(X\downarrow _{N})\end{eqnarray}$$
 $$\begin{eqnarray}L_{i}(Y)\uparrow ^{G}=L_{i}(Y\uparrow ^{G})\quad \text{and}\quad S_{i}(Y)\uparrow ^{G}=S_{i}(Y\uparrow ^{G}).\end{eqnarray}$$
$$\begin{eqnarray}L_{i}(Y)\uparrow ^{G}=L_{i}(Y\uparrow ^{G})\quad \text{and}\quad S_{i}(Y)\uparrow ^{G}=S_{i}(Y\uparrow ^{G}).\end{eqnarray}$$
Proof. Part (a) is a well-known result of Villamayor [Reference Villamayor34] and part (b) follows from (a). ◻
Given a normal subgroup
![]() $H\unlhd G$
and
$H\unlhd G$
and
![]() $\tilde{b}$
a
$\tilde{b}$
a
![]() $p$
-block of
$p$
-block of
![]() $H$
, we will use the group
$H$
, we will use the group
![]() $G[\tilde{b}]$
defined by Dade [Reference Dade7]. A more explicit description of
$G[\tilde{b}]$
defined by Dade [Reference Dade7]. A more explicit description of
![]() $G[\tilde{b}]$
can also be found in [Reference Hida and Koshitani17, Lemma 3.2]. Roughly speaking
$G[\tilde{b}]$
can also be found in [Reference Hida and Koshitani17, Lemma 3.2]. Roughly speaking
![]() $G[\tilde{b}]$
is the stabilizer of
$G[\tilde{b}]$
is the stabilizer of
![]() $\tilde{b}$
as
$\tilde{b}$
as
![]() $k(H\times H)$
-module.
$k(H\times H)$
-module.
Lemma 2.2. (Dade)
Let
![]() $H\unlhd G$
such that
$H\unlhd G$
such that
![]() $p\,\not |\,|G/H|$
, and let
$p\,\not |\,|G/H|$
, and let
![]() $P$
be a Sylow
$P$
be a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $H$
. Let
$H$
. Let
![]() $\tilde{b}=B_{0}(kH)$
and
$\tilde{b}=B_{0}(kH)$
and
![]() $B=B_{0}(kG)$
be the principal blocks of
$B=B_{0}(kG)$
be the principal blocks of
![]() $kH$
and
$kH$
and
![]() $kG$
, respectively. Set
$kG$
, respectively. Set
![]() $N=H\,C_{G}(P)$
. Then the following hold:
$N=H\,C_{G}(P)$
. Then the following hold:
(a) The block
 $\tilde{b}$
is
$\tilde{b}$
is
 $G$
-invariant.
$G$
-invariant.(b)
 $N=G[\tilde{b}]$
and
$N=G[\tilde{b}]$
and
 $N\unlhd G$
.
$N\unlhd G$
.(c) If
 $b$
denotes the principal block of
$b$
denotes the principal block of
 $kN$
, then
$kN$
, then
 $1_{B}=1_{b}$
.
$1_{B}=1_{b}$
.
Proof. (a) Obvious since
![]() $\tilde{b}$
is the principal block. (b) The first claim follows from [Reference Dade7, Corollary 12.6] since
$\tilde{b}$
is the principal block. (b) The first claim follows from [Reference Dade7, Corollary 12.6] since
![]() $\tilde{b}$
is the principal block. Moreover, as
$\tilde{b}$
is the principal block. Moreover, as
![]() $\tilde{b}$
is
$\tilde{b}$
is
![]() $G$
-invariant, the fact that
$G$
-invariant, the fact that
![]() $G[\tilde{b}]\unlhd G$
follows from [Reference Dade7, Proposition 2.17].
$G[\tilde{b}]\unlhd G$
follows from [Reference Dade7, Proposition 2.17].
(c) The main argument to prove (c) is given by [Reference Külshammer27, p. 303 line 10]. We give here a full argument for completeness. As
![]() $\tilde{b}$
is
$\tilde{b}$
is
![]() $G$
-invariant,
$G$
-invariant,
![]() $1_{\tilde{b}}$
is an idempotent of
$1_{\tilde{b}}$
is an idempotent of
![]() $Z(kG)$
and we can write
$Z(kG)$
and we can write
for an integer
![]() $n\geqslant 0$
and for distinct nonprincipal blocks
$n\geqslant 0$
and for distinct nonprincipal blocks
![]() $B_{1},\ldots ,B_{n}$
of
$B_{1},\ldots ,B_{n}$
of
![]() $kG$
. Thus,
$kG$
. Thus,
![]() $1_{\tilde{b}}\,1_{B}=1_{B}$
. Namely,
$1_{\tilde{b}}\,1_{B}=1_{B}$
. Namely,
This implies
![]() $1_{B}\in Z(C)$
since
$1_{B}\in Z(C)$
since
![]() $1_{B}\in Z(kG)$
. Hence it follows from [Reference Külshammer26, Corollary 4] and part (b) that
$1_{B}\in Z(kG)$
. Hence it follows from [Reference Külshammer26, Corollary 4] and part (b) that
where
![]() $\ast$
denotes the crossed product. Thus
$\ast$
denotes the crossed product. Thus
![]() $1_{B}\in Z(kN)$
. On the other hand, since
$1_{B}\in Z(kN)$
. On the other hand, since
![]() $b$
is the principal block of
$b$
is the principal block of
![]() $kN$
, we have
$kN$
, we have
![]() $1_{b}$
is
$1_{b}$
is
![]() $G$
-invariant, so that
$G$
-invariant, so that
![]() $1_{b}\in Z(kG)$
. Hence, as above, we can write
$1_{b}\in Z(kG)$
. Hence, as above, we can write
where
![]() $t\geqslant 0$
is an integer and
$t\geqslant 0$
is an integer and
![]() $B_{1}^{\prime },\cdots \,,B_{t}^{\prime }$
are distinct nonprincipal blocks of
$B_{1}^{\prime },\cdots \,,B_{t}^{\prime }$
are distinct nonprincipal blocks of
![]() $kG$
. Set
$kG$
. Set
![]() $\tilde{e}=1_{b}-1_{B}\in Z(kN)$
(since
$\tilde{e}=1_{b}-1_{B}\in Z(kN)$
(since
![]() $1_{B}\in Z(kN)$
). Therefore
$1_{B}\in Z(kN)$
). Therefore
![]() $1_{b}=1_{B}+\tilde{e}$
is a decomposition of
$1_{b}=1_{B}+\tilde{e}$
is a decomposition of
![]() $1_{b}$
into orthogonal idempotents of
$1_{b}$
into orthogonal idempotents of
![]() $Z(kN)$
. This implies that
$Z(kN)$
. This implies that
![]() $\tilde{e}=0$
, and hence
$\tilde{e}=0$
, and hence
![]() $1_{b}=1_{B}$
.◻
$1_{b}=1_{B}$
.◻
Finally, we will need the following well-known properties of relative projectivity and inflation in direct products. We recall that if
![]() $N\unlhd G$
and
$N\unlhd G$
and
![]() $U$
is a
$U$
is a
![]() $k(G/N)$
-module, then we denote by
$k(G/N)$
-module, then we denote by
![]() $\text{Inf}_{G/N}^{G}(U)$
the inflation of
$\text{Inf}_{G/N}^{G}(U)$
the inflation of
![]() $U$
from
$U$
from
![]() $G/N$
to
$G/N$
to
![]() $G$
, namely
$G$
, namely
![]() $\text{Inf}_{G/N}^{G}(U)=U$
as
$\text{Inf}_{G/N}^{G}(U)=U$
as
![]() $k$
-vector space and becomes a
$k$
-vector space and becomes a
![]() $kG$
-module via the action of
$kG$
-module via the action of
![]() $G$
obtained by composition with the canonical epimorphism
$G$
obtained by composition with the canonical epimorphism
![]() $G{\twoheadrightarrow}G/N$
. Furthermore, if
$G{\twoheadrightarrow}G/N$
. Furthermore, if
![]() $G=N\times H$
is the direct product of two finite groups
$G=N\times H$
is the direct product of two finite groups
![]() $N$
and
$N$
and
![]() $H$
, and
$H$
, and
![]() $U$
and
$U$
and
![]() $V$
, are
$V$
, are
![]() $kN$
- and
$kN$
- and
![]() $kH$
-modules, respectively, then on the one hand
$kH$
-modules, respectively, then on the one hand
![]() $X=U\otimes _{k}V$
becomes a
$X=U\otimes _{k}V$
becomes a
![]() $kG$
-module via the action
$kG$
-module via the action
and on the other hand, setting
![]() $U^{\prime }=\text{Inf}_{G/H\cong N}^{G}(U)$
and
$U^{\prime }=\text{Inf}_{G/H\cong N}^{G}(U)$
and
![]() $V^{\prime }=\text{Inf}_{G/N\cong H}^{G}(V)$
, we have that
$V^{\prime }=\text{Inf}_{G/N\cong H}^{G}(V)$
, we have that
![]() $U^{\prime }\otimes _{k}V^{\prime }$
becomes a
$U^{\prime }\otimes _{k}V^{\prime }$
becomes a
![]() $kG$
-module via the diagonal action
$kG$
-module via the diagonal action
It is then easily seen that
![]() $X\cong U^{\prime }\otimes _{k}V^{\prime }$
as
$X\cong U^{\prime }\otimes _{k}V^{\prime }$
as
![]() $kG$
-modules.
$kG$
-modules.
Lemma 2.3. Assume that
![]() $G=N\times H$
is the direct product of two finite groups
$G=N\times H$
is the direct product of two finite groups
![]() $N$
and
$N$
and
![]() $H$
. Let
$H$
. Let
![]() $U$
be a
$U$
be a
![]() $kN$
-module and
$kN$
-module and
![]() $V$
be a
$V$
be a
![]() $kH$
-module. Set
$kH$
-module. Set
![]() $X=U\otimes _{k}V$
,
$X=U\otimes _{k}V$
,
![]() $U^{\prime }=\text{Inf}_{G/N}^{G}(U)$
and
$U^{\prime }=\text{Inf}_{G/N}^{G}(U)$
and
![]() $V^{\prime }=\text{Inf}_{G/N}^{G}(V)$
. If
$V^{\prime }=\text{Inf}_{G/N}^{G}(V)$
. If
![]() $U$
is projective as a
$U$
is projective as a
![]() $kL$
-module, then
$kL$
-module, then
![]() $X$
is a relatively
$X$
is a relatively
![]() $H$
-projective
$H$
-projective
![]() $kG$
-module.
$kG$
-module.
We give a short proof for completeness.
Proof. First, since
![]() $U$
is a projective
$U$
is a projective
![]() $kN$
-module, it is projective relatively to the trivial subgroup, or equivalently projective relatively to the
$kN$
-module, it is projective relatively to the trivial subgroup, or equivalently projective relatively to the
![]() $kN$
-module
$kN$
-module
![]() $k_{\{1\}}\uparrow ^{N}$
, that is projective relatively to the
$k_{\{1\}}\uparrow ^{N}$
, that is projective relatively to the
![]() $k(G/H)$
-module
$k(G/H)$
-module
![]() $k_{H/H}\uparrow ^{G/H}$
by using the isomorphism
$k_{H/H}\uparrow ^{G/H}$
by using the isomorphism
![]() $N\cong G/H$
. Therefore, by [Reference Lassueur30, Lemma 2.1.1(c)], it follows that the inflated
$N\cong G/H$
. Therefore, by [Reference Lassueur30, Lemma 2.1.1(c)], it follows that the inflated
![]() $kG$
-module
$kG$
-module
![]() $U^{\prime }=\text{Inf}_{G/H}^{G}(U)$
is projective relatively to the inflated
$U^{\prime }=\text{Inf}_{G/H}^{G}(U)$
is projective relatively to the inflated
![]() $kG$
-module
$kG$
-module
 $$\begin{eqnarray}\displaystyle \text{Inf}_{G/H}^{G}(k_{H/H}\uparrow ^{G/H}) & = & \displaystyle \text{Inf}_{G/H}^{G}\circ \text{Ind}_{H/H}^{G/H}(k_{G/H})\nonumber\\ \displaystyle & = & \displaystyle \text{Ind}_{H}^{G}\circ \text{Inf}_{H/H}^{H}(k_{H/H})=k_{H}\uparrow ^{G}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Inf}_{G/H}^{G}(k_{H/H}\uparrow ^{G/H}) & = & \displaystyle \text{Inf}_{G/H}^{G}\circ \text{Ind}_{H/H}^{G/H}(k_{G/H})\nonumber\\ \displaystyle & = & \displaystyle \text{Ind}_{H}^{G}\circ \text{Inf}_{H/H}^{H}(k_{H/H})=k_{H}\uparrow ^{G}\nonumber\end{eqnarray}$$
(where
![]() $\text{Ind}$
denotes the induction seen as a functor). Hence
$\text{Ind}$
denotes the induction seen as a functor). Hence
![]() $U^{\prime }$
is projective relatively to
$U^{\prime }$
is projective relatively to
![]() $H$
. It follows directly that the tensor product
$H$
. It follows directly that the tensor product
![]() $X\cong U^{\prime }\otimes _{k}V^{\prime }$
is
$X\cong U^{\prime }\otimes _{k}V^{\prime }$
is
![]() $H$
-projective, because one of the factors is (see e.g., [Reference Benson3, Corollary 3.6.7]).◻
$H$
-projective, because one of the factors is (see e.g., [Reference Benson3, Corollary 3.6.7]).◻
3 Background results on the Auslander–Reiten quiver
We recall briefly basic facts concerning the stable Auslander–Reiten quiver of a group algebra, which we will be using in the sequel. For a complete introduction to Auslander–Reiten theory, we refer the reader to the textbooks [Reference Auslander, Reiten and Smalø2, Chapter IV] and [Reference Benson3, Chapter 4].
To finish setting up our notation, given a
![]() $kG$
-module
$kG$
-module
![]() $M$
, we denote by
$M$
, we denote by
![]() $\unicode[STIX]{x1D6FA}^{n}(M)~(n\in \mathbb{Z})$
its
$\unicode[STIX]{x1D6FA}^{n}(M)~(n\in \mathbb{Z})$
its
![]() $n$
th Heller translate of
$n$
th Heller translate of
![]() $M$
. Given a simple
$M$
. Given a simple
![]() $kG$
-module
$kG$
-module
![]() $S$
, we denote by
$S$
, we denote by
![]() $P(S)$
its projective cover and by
$P(S)$
its projective cover and by
![]() ${\mathcal{H}}(P(S))$
the heart of
${\mathcal{H}}(P(S))$
the heart of
![]() $P(S)$
, that is
$P(S)$
, that is
![]() ${\mathcal{H}}(P(S))=P(S)J/\text{soc}\,(P(S))$
.
${\mathcal{H}}(P(S))=P(S)J/\text{soc}\,(P(S))$
.
Let
![]() $M$
be an indecomposable
$M$
be an indecomposable
![]() $kG$
-module. By definition, an Auslander–Reiten sequence (or AR-sequence) terminating at
$kG$
-module. By definition, an Auslander–Reiten sequence (or AR-sequence) terminating at
![]() $M$
is a nonsplit short exact sequence
$M$
is a nonsplit short exact sequence
satisfying the following conditions: first
![]() $N$
is indecomposable, and second for each
$N$
is indecomposable, and second for each
![]() $kG$
-homomorphism
$kG$
-homomorphism
![]() $h:X\rightarrow M$
which is not a split epimorphism, there exists a
$h:X\rightarrow M$
which is not a split epimorphism, there exists a
![]() $kG$
-homomorphism
$kG$
-homomorphism
![]() $h^{\prime }:X\rightarrow E$
such that
$h^{\prime }:X\rightarrow E$
such that
![]() $h=gh^{\prime }$
. Given an indecomposable nonprojective
$h=gh^{\prime }$
. Given an indecomposable nonprojective
![]() $kG$
-module
$kG$
-module
![]() $M$
, there exists always an
$M$
, there exists always an
![]() $AR$
-sequence terminating at
$AR$
-sequence terminating at
![]() $M$
, and it is unique up to isomorphism of short exact sequences. Moreover, since
$M$
, and it is unique up to isomorphism of short exact sequences. Moreover, since
![]() $kG$
is a finite-dimensional symmetric Algebra, we have
$kG$
is a finite-dimensional symmetric Algebra, we have
![]() $N\cong \unicode[STIX]{x1D6FA}^{2}(M)$
(see [Reference Benson3, 4.12.8]). In similar fashion, there exists an AR-sequence starting at
$N\cong \unicode[STIX]{x1D6FA}^{2}(M)$
(see [Reference Benson3, 4.12.8]). In similar fashion, there exists an AR-sequence starting at
![]() $M$
, unique up to isomorphism of short exact sequences, with end term isomorphic to
$M$
, unique up to isomorphism of short exact sequences, with end term isomorphic to
![]() $\unicode[STIX]{x1D6FA}^{-2}(M)$
. For a nonprojective simple
$\unicode[STIX]{x1D6FA}^{-2}(M)$
. For a nonprojective simple
![]() $kG$
-module
$kG$
-module
![]() $S$
, the Auslander–Reiten sequence terminating at
$S$
, the Auslander–Reiten sequence terminating at
![]() $\unicode[STIX]{x1D6FA}^{-1}(S)$
is of the form
$\unicode[STIX]{x1D6FA}^{-1}(S)$
is of the form
and is called the standard sequence associated to
![]() $S$
. This is the unique
$S$
. This is the unique
![]() $AR$
-sequence in which the PIM
$AR$
-sequence in which the PIM
![]() $P(S)$
occurs.
$P(S)$
occurs.
The Auslander–Reiten quiver (or AR-quiver) of
![]() $kG$
(resp. of a
$kG$
(resp. of a
![]() $p$
-block
$p$
-block
![]() $B$
of
$B$
of
![]() $kG$
) is the directed graph
$kG$
) is the directed graph
![]() $\unicode[STIX]{x1D6E4}(kG)$
(resp.
$\unicode[STIX]{x1D6E4}(kG)$
(resp.
![]() $\unicode[STIX]{x1D6E4}(B)$
) whose vertices are the isomorphism classes of indecomposable
$\unicode[STIX]{x1D6E4}(B)$
) whose vertices are the isomorphism classes of indecomposable
![]() $kG$
-modules (resp.
$kG$
-modules (resp.
![]() $B$
-modules), and the number of arrows between two indecomposable modules
$B$
-modules), and the number of arrows between two indecomposable modules
![]() $M$
and
$M$
and
![]() $N$
corresponds to the dimension of the space of irreducible maps between
$N$
corresponds to the dimension of the space of irreducible maps between
![]() $M$
and
$M$
and
![]() $N$
. We refer the reader to [Reference Auslander, Reiten and Smalø2, Chapter IV] for a precise definition. Then the stable Auslander–Reiten quiver of
$N$
. We refer the reader to [Reference Auslander, Reiten and Smalø2, Chapter IV] for a precise definition. Then the stable Auslander–Reiten quiver of
![]() $kG$
(resp. of
$kG$
(resp. of
![]() $B$
) is obtained from
$B$
) is obtained from
![]() $\unicode[STIX]{x1D6E4}(kG)$
(resp.
$\unicode[STIX]{x1D6E4}(kG)$
(resp.
![]() $\unicode[STIX]{x1D6E4}(B)$
) by removing the vertices corresponding to projective modules and all arrows attached to these vertices; it is denoted by
$\unicode[STIX]{x1D6E4}(B)$
) by removing the vertices corresponding to projective modules and all arrows attached to these vertices; it is denoted by
![]() $\unicode[STIX]{x1D6E4}_{s}(kG)$
(resp.
$\unicode[STIX]{x1D6E4}_{s}(kG)$
(resp.
![]() $\unicode[STIX]{x1D6E4}_{s}(B)$
). By convention, we use the terminology AR-component to refer to a connected component of
$\unicode[STIX]{x1D6E4}_{s}(B)$
). By convention, we use the terminology AR-component to refer to a connected component of
![]() $\unicode[STIX]{x1D6E4}_{s}(kG)$
, and we denote by
$\unicode[STIX]{x1D6E4}_{s}(kG)$
, and we denote by
![]() $\unicode[STIX]{x1D6E4}_{s}(M)$
the connected component of
$\unicode[STIX]{x1D6E4}_{s}(M)$
the connected component of
![]() $\unicode[STIX]{x1D6E4}_{s}(kG)$
containing a given indecomposable
$\unicode[STIX]{x1D6E4}_{s}(kG)$
containing a given indecomposable
![]() $kG$
-module
$kG$
-module
![]() $M$
.
$M$
.
Erdmann [Reference Erdmann11] proved that all components of the stable Auslander–Reiten quiver belonging to a wild block have tree class
![]() $A_{\infty }$
, that is of the form
$A_{\infty }$
, that is of the form
![]() $\mathbb{Z}A_{\infty }$
or infinite tubes
$\mathbb{Z}A_{\infty }$
or infinite tubes
![]() $\mathbb{Z}A_{\infty }/\langle \unicode[STIX]{x1D70F}^{a}\rangle$
of rank
$\mathbb{Z}A_{\infty }/\langle \unicode[STIX]{x1D70F}^{a}\rangle$
of rank
![]() $a$
, where
$a$
, where
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FA}^{2}$
is the Auslander–Reiten shift. In a component with tree class
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FA}^{2}$
is the Auslander–Reiten shift. In a component with tree class
![]() $A_{\infty }$
an indecomposable nonprojective
$A_{\infty }$
an indecomposable nonprojective
![]() $kG$
-module
$kG$
-module
![]() $M$
is said to lie at the end (or on the rim) of its AR-component if the projective-free part of the middle term
$M$
is said to lie at the end (or on the rim) of its AR-component if the projective-free part of the middle term
![]() $X_{M}$
of the Auslander–Reiten sequence
$X_{M}$
of the Auslander–Reiten sequence
terminating at
![]() $M$
is indecomposable. In this setup, clearly a simple module
$M$
is indecomposable. In this setup, clearly a simple module
![]() $S$
lies at the end of its component if and only if
$S$
lies at the end of its component if and only if
![]() ${\mathcal{H}}(P(S))$
is indecomposable, and
${\mathcal{H}}(P(S))$
is indecomposable, and
![]() $S$
lies in a tube if and only if
$S$
lies in a tube if and only if
![]() $S$
is periodic (i.e.,
$S$
is periodic (i.e.,
![]() $\unicode[STIX]{x1D6FA}$
-periodic). We also recall that for a selfinjective algebra the shape of the components of the stable Auslander–Reiten quiver is an invariant of its Morita equivalence class. By the above, the property of lying on the rim of its AR-component for a nonprojective simple module is also invariant under Morita equivalence.
$\unicode[STIX]{x1D6FA}$
-periodic). We also recall that for a selfinjective algebra the shape of the components of the stable Auslander–Reiten quiver is an invariant of its Morita equivalence class. By the above, the property of lying on the rim of its AR-component for a nonprojective simple module is also invariant under Morita equivalence.
Simple
![]() $kG$
-modules are known to lie on the rim of their
$kG$
-modules are known to lie on the rim of their
![]() $AR$
-components in the following cases:
$AR$
-components in the following cases:
Theorem 3.1. Let
![]() $B$
be a wild
$B$
be a wild
![]() $p$
-block of
$p$
-block of
![]() $kG$
. Then every simple
$kG$
. Then every simple
![]() $B$
-module lies at the end of its AR-component in all of the following cases:
$B$
-module lies at the end of its AR-component in all of the following cases:
(a)
 $G$
has a nontrivial normal
$G$
has a nontrivial normal
 $p$
-subgroup [Reference Kawata20, Theorem 2.1];
$p$
-subgroup [Reference Kawata20, Theorem 2.1];(b)
 $G$
is
$G$
is
 $p$
-solvable [Reference Kawata20, Corollary 2.2];
$p$
-solvable [Reference Kawata20, Corollary 2.2];(c)
 $G$
is a perfect finite group of Lie type in the defining characteristic and
$G$
is a perfect finite group of Lie type in the defining characteristic and
 $B$
has full defect [Reference Kawata, Michler and Uno22, Theorem];
$B$
has full defect [Reference Kawata, Michler and Uno22, Theorem];(d)
 $G$
has an abelian Sylow
$G$
has an abelian Sylow
 $2$
-subgroup and
$2$
-subgroup and
 $B$
is the principal
$B$
is the principal
 $2$
-block [Reference Kawata, Michler and Uno21, Theorem 5];
$2$
-block [Reference Kawata, Michler and Uno21, Theorem 5];(e)
 $G$
is a symmetric group or an alternating group [Reference Bessenrodt and Uno4, Theorems 5.3 and 5.5];
$G$
is a symmetric group or an alternating group [Reference Bessenrodt and Uno4, Theorems 5.3 and 5.5];(f)
 $p=2$
and
$p=2$
and
 $G$
is a Schur cover of a symmetric group or of an alternating group [Reference Bessenrodt and Uno4, Theorems 5.3 and 5.5];
$G$
is a Schur cover of a symmetric group or of an alternating group [Reference Bessenrodt and Uno4, Theorems 5.3 and 5.5];(g)
 $p\,\not =\,2$
and
$p\,\not =\,2$
and
 $G$
is a Schur cover of a symmetric group or of an alternating group such that the defect of
$G$
is a Schur cover of a symmetric group or of an alternating group such that the defect of
 $B$
is at least
$B$
is at least
 $3$
[Reference Bessenrodt and Uno4, Theorems 5.3 and 5.5].
$3$
[Reference Bessenrodt and Uno4, Theorems 5.3 and 5.5].
Moreover, we will use the following computational criterion throughout:
Theorem 3.2. (Kawata’s Criterion on Cartan matrices [Reference Kawata20, Theorem 1.5])
Let
![]() $B$
be a wild
$B$
be a wild
![]() $p$
-block of
$p$
-block of
![]() $kG$
. Suppose that there exists a simple
$kG$
. Suppose that there exists a simple
![]() $B$
-module
$B$
-module
![]() $S$
lying on the
$S$
lying on the
![]() $n$
th row from the end of
$n$
th row from the end of
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
, where
$\unicode[STIX]{x1D6E4}_{s}(S)$
, where
![]() $n\geqslant 2$
is minimal with this property. Then there exist pairwise nonisomorphic simple
$n\geqslant 2$
is minimal with this property. Then there exist pairwise nonisomorphic simple
![]() $B$
-modules
$B$
-modules
![]() $S_{2},\ldots ,S_{n}$
with the following properties:
$S_{2},\ldots ,S_{n}$
with the following properties:
(a) for each
 $2\leqslant i\leqslant n$
, we have that
$2\leqslant i\leqslant n$
, we have that
 $S_{i}\cong \unicode[STIX]{x1D6FA}^{2(i-2)}(S_{2})$
and
$S_{i}\cong \unicode[STIX]{x1D6FA}^{2(i-2)}(S_{2})$
and
 $S_{i}$
lies at the end of
$S_{i}$
lies at the end of
 $\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
;
$\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
;(b) the projective covers of
 $P(S_{i})$
of the simple modules
$P(S_{i})$
of the simple modules
 $S_{i}~(2\leqslant i\leqslant n)$
are uniserial of length
$S_{i}~(2\leqslant i\leqslant n)$
are uniserial of length
 $n+1$
with the following Loewy structure:The Cartan matrix of
$n+1$
with the following Loewy structure:The Cartan matrix of
 $B$
is given by where the columns are labeled by
$B$
is given by where the columns are labeled by $$\begin{eqnarray}\left(\begin{array}{@{}cccccccc@{}}2 & 1 & \cdots \, & \cdots \, & 1 & 0 & \cdots \, & 0\\ 1 & 2 & \ddots & & \vdots & \vdots & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots & \vdots & & \vdots \\ \vdots & & \ddots & 2 & 1 & 0 & \cdots \, & 0\\ 1 & \cdots \, & \cdots \, & 1 & \ast & \cdots \, & \cdots \, & \ast \\ 0 & \cdots \, & \cdots \, & 0 & \vdots & & & \vdots \\ \vdots & & & \vdots & \vdots & & & \vdots \\ 0 & \cdots \, & \cdots \, & 0 & \ast & \cdots \, & \cdots \, & \ast \end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccccccc@{}}2 & 1 & \cdots \, & \cdots \, & 1 & 0 & \cdots \, & 0\\ 1 & 2 & \ddots & & \vdots & \vdots & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots & \vdots & & \vdots \\ \vdots & & \ddots & 2 & 1 & 0 & \cdots \, & 0\\ 1 & \cdots \, & \cdots \, & 1 & \ast & \cdots \, & \cdots \, & \ast \\ 0 & \cdots \, & \cdots \, & 0 & \vdots & & & \vdots \\ \vdots & & & \vdots & \vdots & & & \vdots \\ 0 & \cdots \, & \cdots \, & 0 & \ast & \cdots \, & \cdots \, & \ast \end{array}\right),\end{eqnarray}$$
 $S_{n},\ldots ,S_{2},S,\ldots$
in this order.
$S_{n},\ldots ,S_{2},S,\ldots$
in this order.
Remark 3.3.
(a) If the Cartan matrix of a block has the shape of Theorem 3.2(b) above with
 $n=2$
, then the simple module
$n=2$
, then the simple module
 $S$
corresponding to the second column lies on the 2nd row of its AR-component. Indeed in this case
$S$
corresponding to the second column lies on the 2nd row of its AR-component. Indeed in this case  and the standard sequence associated to
and the standard sequence associated to
 $S_{2}$
is so that
$S_{2}$
is so that $$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6FA}(S_{2})\rightarrow S\oplus P(S_{2})\rightarrow \unicode[STIX]{x1D6FA}^{-1}(S_{2})\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6FA}(S_{2})\rightarrow S\oplus P(S_{2})\rightarrow \unicode[STIX]{x1D6FA}^{-1}(S_{2})\rightarrow 0,\end{eqnarray}$$
 $S_{2}$
lies at the end of its AR-component and
$S_{2}$
lies at the end of its AR-component and
 $S$
on the 2nd row of its AR-component.
$S$
on the 2nd row of its AR-component.A converse to Kawata’s Criterion need not be true in general for an
 $n\geqslant 3$
.
$n\geqslant 3$
.(b) The above was used to produce two counterexamples of simple modules not lying at the end of their AR-components. Namely, the group
 $F_{4}(2)$
for
$F_{4}(2)$
for
 $p=5$
has a simple module in the principal block of dimension 875823 lying on the 2nd row of its AR-component, and the group
$p=5$
has a simple module in the principal block of dimension 875823 lying on the 2nd row of its AR-component, and the group
 $2.Ru$
for
$2.Ru$
for
 $p=3$
has a faithful simple module also lying on the 2nd row. See [Reference Kawata, Michler and Uno22, §4]. Both counterexamples are obtained thanks to the decomposition matrices of these groups computed by Hiß.
$p=3$
has a faithful simple module also lying on the 2nd row. See [Reference Kawata, Michler and Uno22, §4]. Both counterexamples are obtained thanks to the decomposition matrices of these groups computed by Hiß.
We can now improve Kawata’s result by describing more accurately the structure of the heart of the projective cover of the simple module
![]() $S$
lying on the
$S$
lying on the
![]() $n$
th row of its AR-component.
$n$
th row of its AR-component.
Corollary 3.4. With the assumptions and the notation of Theorem 3.2, we have that the heart of the projective cover of the simple module
![]() $S$
is decomposable and has a uniserial indecomposable summand of length
$S$
is decomposable and has a uniserial indecomposable summand of length
![]() $n-1$
. More precisely
$n-1$
. More precisely

where
![]() $V$
is an indecomposable
$V$
is an indecomposable
![]() $kG$
-module.
$kG$
-module.
Proof. First, since by assumption the module
![]() $S$
does not lie at the end of its AR-component, which is of tree class
$S$
does not lie at the end of its AR-component, which is of tree class
![]() $A_{\infty }$
, it is clear that the heart of the projective cover of
$A_{\infty }$
, it is clear that the heart of the projective cover of
![]() $S$
must be the direct sum of two indecomposable direct summands, say
$S$
must be the direct sum of two indecomposable direct summands, say
Using [Reference Kawata20, Proposition 1.4], we have that the part of the component
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
below
$\unicode[STIX]{x1D6E4}_{s}(S)$
below
![]() $S$
is as follows:
$S$
is as follows:

Therefore, using the fact that the Heller operator
![]() $\unicode[STIX]{x1D6FA}$
induces a graph isomorphism from
$\unicode[STIX]{x1D6FA}$
induces a graph isomorphism from
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
to
$\unicode[STIX]{x1D6E4}_{s}(S)$
to
![]() $\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
, we have that in
$\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
, we have that in
![]() $\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
the diamond corresponding to the standard sequence associated to
$\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
the diamond corresponding to the standard sequence associated to
![]() $S$
is as follows:
$S$
is as follows:

Hence it suffices to compute ![]()
Since the top of the uniserial module ![]() is
is
![]() $S_{n}$
, the projective cover of
$S_{n}$
, the projective cover of ![]() must be
must be
![]() $P(S_{n})$
. Hence taking the kernel of the canonical surjection
$P(S_{n})$
. Hence taking the kernel of the canonical surjection ![]() we obtain from the Loewy series of the PIM
we obtain from the Loewy series of the PIM
![]() $P(S_{n})$
in Theorem 3.2(c) that
$P(S_{n})$
in Theorem 3.2(c) that
![]() $U$
has the following Loewy series
$U$
has the following Loewy series

4 Groups having a solvable quotient of
 $p^{\prime }$
-order
$p^{\prime }$
-order
Throughout this section, we will assume that the following hypotheses hold:
Hypothesis 4.1. Assume that:
(a)
 $G$
is a finite group of order divisible by
$G$
is a finite group of order divisible by
 $p$
and
$p$
and
 $N\unlhd G$
is a normal subgroup such that
$N\unlhd G$
is a normal subgroup such that
 $|G/N|=:q$
is a prime number with
$|G/N|=:q$
is a prime number with
 $q\neq p$
, and we set
$q\neq p$
, and we set
 $G/N=:\langle gN\rangle$
for an element
$G/N=:\langle gN\rangle$
for an element
 $g\in G\backslash N$
.
$g\in G\backslash N$
.(b)
 $B$
and
$B$
and
 $b$
are wild blocks of
$b$
are wild blocks of
 $kG$
and
$kG$
and
 $kN$
, respectively, such that
$kN$
, respectively, such that
 $1_{B}=1_{b}$
.
$1_{B}=1_{b}$
.
Lemma 4.2. Assume Hypothesis 4.1 holds. Let
![]() $\unicode[STIX]{x1D701}\in k^{\times }$
be a primitive
$\unicode[STIX]{x1D701}\in k^{\times }$
be a primitive
![]() $q$
th root of unity in
$q$
th root of unity in
![]() $k$
, and for each
$k$
, and for each
![]() $1\leqslant j\leqslant q$
let
$1\leqslant j\leqslant q$
let
![]() $Z_{j}$
be the one-dimensional
$Z_{j}$
be the one-dimensional
![]() $k(G/N)$
-module defined by
$k(G/N)$
-module defined by
![]() $Z_{j}=\langle \unicode[STIX]{x1D6FC}_{j}\rangle _{k}$
and
$Z_{j}=\langle \unicode[STIX]{x1D6FC}_{j}\rangle _{k}$
and
![]() $\unicode[STIX]{x1D6FC}_{j}\cdot gN=\unicode[STIX]{x1D701}^{j-1}\unicode[STIX]{x1D6FC}_{j}$
, so that in particular
$\unicode[STIX]{x1D6FC}_{j}\cdot gN=\unicode[STIX]{x1D701}^{j-1}\unicode[STIX]{x1D6FC}_{j}$
, so that in particular
![]() $Z_{1}=k_{G/N}$
. The following holds:
$Z_{1}=k_{G/N}$
. The following holds:
(a) If
 ${\mathcal{S}}\in \text{IBr}(B)$
is such that
${\mathcal{S}}\in \text{IBr}(B)$
is such that
 ${\mathcal{S}}\downarrow _{N}$
is not simple, then for each
${\mathcal{S}}\downarrow _{N}$
is not simple, then for each
 $1\leqslant j\leqslant q$
, as
$1\leqslant j\leqslant q$
, as $$\begin{eqnarray}{\mathcal{S}}\otimes _{k}Z_{j}\cong {\mathcal{S}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}\otimes _{k}Z_{j}\cong {\mathcal{S}}\end{eqnarray}$$
 $kG$
-modules, where we see
$kG$
-modules, where we see
 $Z_{j}$
as a
$Z_{j}$
as a
 $kG$
-module via inflation.
$kG$
-module via inflation.(b) There are integers
 $m\geqslant 1$
and
$m\geqslant 1$
and
 $\ell \geqslant 0$
such that where for each
$\ell \geqslant 0$
such that where for each $$\begin{eqnarray}\displaystyle \text{IBr}(B) & = & \displaystyle \{{\mathcal{S}}_{ij}\,|\,1\leqslant i\leqslant m;1\leqslant j\leqslant q\}\bigsqcup \,\{{\mathcal{S}}_{i}\,|\,m+1\leqslant i\leqslant m+\ell \}\quad \text{and}\nonumber\\ \displaystyle \text{IBr}(b) & = & \displaystyle \{{\mathcal{T}}_{i}\,|\,1\leqslant i\leqslant m\}\,\bigsqcup \,\{{\mathcal{T}}_{ij}\,|\,m+1\leqslant i\leqslant m+\ell ,1\leqslant j\leqslant q\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{IBr}(B) & = & \displaystyle \{{\mathcal{S}}_{ij}\,|\,1\leqslant i\leqslant m;1\leqslant j\leqslant q\}\bigsqcup \,\{{\mathcal{S}}_{i}\,|\,m+1\leqslant i\leqslant m+\ell \}\quad \text{and}\nonumber\\ \displaystyle \text{IBr}(b) & = & \displaystyle \{{\mathcal{T}}_{i}\,|\,1\leqslant i\leqslant m\}\,\bigsqcup \,\{{\mathcal{T}}_{ij}\,|\,m+1\leqslant i\leqslant m+\ell ,1\leqslant j\leqslant q\},\nonumber\end{eqnarray}$$
 $1\leqslant i\leqslant m$
and each
$1\leqslant i\leqslant m$
and each
 $1\leqslant j\leqslant q$
, and for each
$1\leqslant j\leqslant q$
, and for each $$\begin{eqnarray}{\mathcal{S}}_{ij}\downarrow _{N}={\mathcal{T}}_{i}\quad \text{and}\quad {\mathcal{T}}_{i}\uparrow ^{G}={\mathcal{S}}_{i1}\oplus \cdots \oplus {\mathcal{S}}_{iq},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}_{ij}\downarrow _{N}={\mathcal{T}}_{i}\quad \text{and}\quad {\mathcal{T}}_{i}\uparrow ^{G}={\mathcal{S}}_{i1}\oplus \cdots \oplus {\mathcal{S}}_{iq},\end{eqnarray}$$
 $m+1\leqslant i\leqslant m+\ell$
and each
$m+1\leqslant i\leqslant m+\ell$
and each
 $1\leqslant j\leqslant q$
, where we may assume that
$1\leqslant j\leqslant q$
, where we may assume that $$\begin{eqnarray}{\mathcal{S}}_{i}\downarrow _{N}={\mathcal{T}}_{i1}\oplus {\mathcal{T}}_{i2}\oplus \cdots \oplus {\mathcal{T}}_{iq}\quad \text{and}\quad {\mathcal{T}}_{ij}\uparrow ^{G}={\mathcal{S}}_{i}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}_{i}\downarrow _{N}={\mathcal{T}}_{i1}\oplus {\mathcal{T}}_{i2}\oplus \cdots \oplus {\mathcal{T}}_{iq}\quad \text{and}\quad {\mathcal{T}}_{ij}\uparrow ^{G}={\mathcal{S}}_{i}\end{eqnarray}$$
 ${\mathcal{T}}_{ij}={{\mathcal{T}}_{i1}}^{g^{j-1}}$
.
${\mathcal{T}}_{ij}={{\mathcal{T}}_{i1}}^{g^{j-1}}$
.Moreover, we can assume that for each
 $1\leqslant j\leqslant q$
,
$1\leqslant j\leqslant q$
,  $$\begin{eqnarray}{\mathcal{S}}_{ij}={\mathcal{S}}_{i1}\otimes _{k}Z_{j}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}_{ij}={\mathcal{S}}_{i1}\otimes _{k}Z_{j}.\end{eqnarray}$$
Proof. (a) Let
![]() $1\leqslant j\leqslant q$
. By assumption and Clifford’s theory we have that
$1\leqslant j\leqslant q$
. By assumption and Clifford’s theory we have that
for some
![]() ${\mathcal{T}}\in \text{IBr}(b)$
. Hence
${\mathcal{T}}\in \text{IBr}(b)$
. Hence
![]() ${\mathcal{T}}\uparrow ^{G}\cong {\mathcal{S}}$
, and
${\mathcal{T}}\uparrow ^{G}\cong {\mathcal{S}}$
, and
![]() ${\mathcal{T}}\uparrow ^{G}\cong {\mathcal{S}}\otimes _{k}Z_{j}$
for each
${\mathcal{T}}\uparrow ^{G}\cong {\mathcal{S}}\otimes _{k}Z_{j}$
for each
![]() $1\leqslant j\leqslant q$
.
$1\leqslant j\leqslant q$
.
(b) As by Hypothesis 4.1 the quotient
![]() $G/N$
is cyclic, the claim follows from the result of Schur and Clifford [Reference Nagao and Tsushima31, Chapter 3, Corollary 5.9 and Problem 11(i)].◻
$G/N$
is cyclic, the claim follows from the result of Schur and Clifford [Reference Nagao and Tsushima31, Chapter 3, Corollary 5.9 and Problem 11(i)].◻
Lemma 4.3. Assume Hypothesis 4.1 holds. Let
![]() ${\mathcal{S}}\in \text{IBr}(B)$
.
${\mathcal{S}}\in \text{IBr}(B)$
.
(a) If
 ${\mathcal{S}}\downarrow _{N}=:{\mathcal{T}}$
is simple, then
${\mathcal{S}}\downarrow _{N}=:{\mathcal{T}}$
is simple, then
 $P({\mathcal{S}})\downarrow _{N}\cong P({\mathcal{T}})$
and
$P({\mathcal{S}})\downarrow _{N}\cong P({\mathcal{T}})$
and
 ${\mathcal{H}}(P({\mathcal{S}}))\downarrow _{N}\cong {\mathcal{H}}(P({\mathcal{T}}))$
.
${\mathcal{H}}(P({\mathcal{S}}))\downarrow _{N}\cong {\mathcal{H}}(P({\mathcal{T}}))$
.(b) If
 ${\mathcal{S}}\downarrow _{N}$
is not simple, then we can write
${\mathcal{S}}\downarrow _{N}$
is not simple, then we can write
 ${\mathcal{S}}\downarrow _{N}={\mathcal{T}}_{1}\oplus {\mathcal{T}}_{2}\oplus \cdots \oplus {\mathcal{T}}_{q}$
with
${\mathcal{S}}\downarrow _{N}={\mathcal{T}}_{1}\oplus {\mathcal{T}}_{2}\oplus \cdots \oplus {\mathcal{T}}_{q}$
with
 ${\mathcal{T}}_{j}={{\mathcal{T}}_{1}}^{g^{j-1}}$
for each
${\mathcal{T}}_{j}={{\mathcal{T}}_{1}}^{g^{j-1}}$
for each
 $1\leqslant j\leqslant q$
and we have that
$1\leqslant j\leqslant q$
and we have that  $$\begin{eqnarray}P({\mathcal{S}})\downarrow _{N}\cong P({\mathcal{T}}_{1})\oplus \cdots \oplus P({\mathcal{T}}_{q})\quad \text{and}\quad {\mathcal{H}}(P({\mathcal{S}}))\downarrow _{N}\cong \bigoplus _{j=1}^{q}{\mathcal{H}}(P({\mathcal{T}}_{j})).\end{eqnarray}$$
$$\begin{eqnarray}P({\mathcal{S}})\downarrow _{N}\cong P({\mathcal{T}}_{1})\oplus \cdots \oplus P({\mathcal{T}}_{q})\quad \text{and}\quad {\mathcal{H}}(P({\mathcal{S}}))\downarrow _{N}\cong \bigoplus _{j=1}^{q}{\mathcal{H}}(P({\mathcal{T}}_{j})).\end{eqnarray}$$
Proof. (a) Obviously
 $$\begin{eqnarray}\displaystyle {\mathcal{T}} & = & \displaystyle {\mathcal{S}}\downarrow _{N}=(P({\mathcal{S}})/P({\mathcal{S}})J)\downarrow _{N}=P({\mathcal{S}})\downarrow _{N}/(P({\mathcal{S}})J)\downarrow _{N}\nonumber\\ \displaystyle & = & \displaystyle P({\mathcal{S}})\downarrow _{N}/(P({\mathcal{S}})\,kG\tilde{J})\text{ by Lemma 2.1}\nonumber\\ \displaystyle & = & \displaystyle P({\mathcal{S}})\downarrow _{N}/P({\mathcal{S}})\downarrow _{N}\,\tilde{J}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{T}} & = & \displaystyle {\mathcal{S}}\downarrow _{N}=(P({\mathcal{S}})/P({\mathcal{S}})J)\downarrow _{N}=P({\mathcal{S}})\downarrow _{N}/(P({\mathcal{S}})J)\downarrow _{N}\nonumber\\ \displaystyle & = & \displaystyle P({\mathcal{S}})\downarrow _{N}/(P({\mathcal{S}})\,kG\tilde{J})\text{ by Lemma 2.1}\nonumber\\ \displaystyle & = & \displaystyle P({\mathcal{S}})\downarrow _{N}/P({\mathcal{S}})\downarrow _{N}\,\tilde{J}.\nonumber\end{eqnarray}$$
Hence the top of
![]() $P({\mathcal{S}})\downarrow _{N}$
is
$P({\mathcal{S}})\downarrow _{N}$
is
![]() ${\mathcal{T}}$
, which implies that
${\mathcal{T}}$
, which implies that
![]() $P({\mathcal{S}})\downarrow _{N}\cong P({\mathcal{T}})$
. Therefore,
$P({\mathcal{S}})\downarrow _{N}\cong P({\mathcal{T}})$
. Therefore,
(b) Similar to (a). ◻
Proposition 4.4. Assume Hypothesis 4.1 holds. If every simple module
![]() $T\in \text{IBr}(b)$
lies at the end of its AR-component, then every simple module
$T\in \text{IBr}(b)$
lies at the end of its AR-component, then every simple module
![]() $S\in \text{IBr}(B)$
lies at the end of its AR-component.
$S\in \text{IBr}(B)$
lies at the end of its AR-component.
Proof. Let
![]() $S\in \text{IBr}(B)$
be a simple module. First assume that
$S\in \text{IBr}(B)$
be a simple module. First assume that
![]() $S\downarrow _{N}=:T\in \text{IBr}(b)$
is simple. Then by Lemma 4.3(a)
$S\downarrow _{N}=:T\in \text{IBr}(b)$
is simple. Then by Lemma 4.3(a)
But by assumption
![]() ${\mathcal{H}}(P(T))$
is indecomposable, therefore so is
${\mathcal{H}}(P(T))$
is indecomposable, therefore so is
![]() ${\mathcal{H}}(P(S))$
.
${\mathcal{H}}(P(S))$
.
We assume now for the rest of the proof that
![]() $S\downarrow _{N}$
is not simple. If
$S\downarrow _{N}$
is not simple. If
![]() $S$
lies at the end of its AR-component, then there is nothing to do. Therefore we now also assume that
$S$
lies at the end of its AR-component, then there is nothing to do. Therefore we now also assume that
![]() $S$
lies on the
$S$
lies on the
![]() $n$
th row from the bottom of
$n$
th row from the bottom of
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
for an integer
$\unicode[STIX]{x1D6E4}_{s}(S)$
for an integer
![]() $n\geqslant 2$
, minimal (as in Kawata’s Criterion on Cartan matrices). By Lemma 4.2(b),
$n\geqslant 2$
, minimal (as in Kawata’s Criterion on Cartan matrices). By Lemma 4.2(b),
where
![]() $T_{1j}={T_{11}}^{g^{j-1}}$
for
$T_{1j}={T_{11}}^{g^{j-1}}$
for
![]() $1\leqslant j\leqslant q$
are nonisomorphic simple modules in
$1\leqslant j\leqslant q$
are nonisomorphic simple modules in
![]() $\text{IBr}(b)$
. We also set
$\text{IBr}(b)$
. We also set
![]() $T_{1}=T_{11}$
.
$T_{1}=T_{11}$
.
Let
![]() $S_{2},\ldots ,S_{n}$
be the simple modules given by Theorem 3.2.
$S_{2},\ldots ,S_{n}$
be the simple modules given by Theorem 3.2.
Claim 1. If the modules
![]() $S_{2}\downarrow _{N},\ldots ,S_{n}\downarrow _{N}$
are all nonsimple, then we have a contradiction.
$S_{2}\downarrow _{N},\ldots ,S_{n}\downarrow _{N}$
are all nonsimple, then we have a contradiction.
Proof of Claim 1.
By assumption and Lemma 4.2, we can write
For each
![]() $2\leqslant i\leqslant n$
we define
$2\leqslant i\leqslant n$
we define
![]() $T_{i}\in \text{IBr}(b)$
by
$T_{i}\in \text{IBr}(b)$
by
![]() $T_{ij}={T_{i}}^{g^{j-1}}$
, where
$T_{ij}={T_{i}}^{g^{j-1}}$
, where
![]() $1\leqslant j\leqslant q$
. We claim that
$1\leqslant j\leqslant q$
. We claim that

Indeed, we know by Theorem 3.2(b) and Lemma 4.3(b) that

where the boxes mean the Loewy and socle series of the
![]() $kN$
-modules. Since the left-hand side is a direct sum of exactly
$kN$
-modules. Since the left-hand side is a direct sum of exactly
![]() $q$
indecomposable
$q$
indecomposable
![]() $kN$
-modules that are
$kN$
-modules that are
![]() $\langle g\rangle$
-conjugate to each other, by interchanging the indices of
$\langle g\rangle$
-conjugate to each other, by interchanging the indices of
![]() $T_{3},\ldots ,T_{n},T_{1}$
desired, we may assume that the PIM
$T_{3},\ldots ,T_{n},T_{1}$
desired, we may assume that the PIM
![]() $P(T_{2})$
has the desired structure. Then automatically the structures of
$P(T_{2})$
has the desired structure. Then automatically the structures of
![]() $P(T_{3}),\ldots ,P(T_{n})$
are as claimed. ◻
$P(T_{3}),\ldots ,P(T_{n})$
are as claimed. ◻
Now, using a similar argument as above, we also obtain

for a
![]() $kG$
-module
$kG$
-module
![]() $V$
where the last equality holds by Corollary 3.4. Hence we have
$V$
where the last equality holds by Corollary 3.4. Hence we have

since
![]() $P(T_{2}),\ldots ,P(T_{n})$
are uniserial by the above.
$P(T_{2}),\ldots ,P(T_{n})$
are uniserial by the above.
But we are assuming that
![]() $T_{2},\ldots ,T_{n}$
lie at the end of their AR-components, so that
$T_{2},\ldots ,T_{n}$
lie at the end of their AR-components, so that
![]() ${\mathcal{H}}(P(T_{2})),\ldots ,{\mathcal{H}}(P(T_{n}))$
are indecomposable. Further
${\mathcal{H}}(P(T_{2})),\ldots ,{\mathcal{H}}(P(T_{n}))$
are indecomposable. Further
![]() ${\mathcal{H}}(P(T_{1}))$
is also indecomposable since
${\mathcal{H}}(P(T_{1}))$
is also indecomposable since
![]() $T_{1}$
lies at the end of its AR-connected component. Therefore the right-hand side term in the latter equation has exactly
$T_{1}$
lies at the end of its AR-connected component. Therefore the right-hand side term in the latter equation has exactly
![]() $q$
indecomposable direct summands. This implies that
$q$
indecomposable direct summands. This implies that
![]() $V=\{0\}$
, hence a contradiction.
$V=\{0\}$
, hence a contradiction.
Claim 2. If the modules
![]() $S_{2}\downarrow _{N},\ldots ,S_{n}\downarrow _{N}$
are all simple, then we have a contradiction.
$S_{2}\downarrow _{N},\ldots ,S_{n}\downarrow _{N}$
are all simple, then we have a contradiction.
Proof of Claim 2.
Set
![]() $T_{i}=S_{i}\downarrow _{N}$
for
$T_{i}=S_{i}\downarrow _{N}$
for
![]() $2\leqslant i\leqslant n$
. We have
$2\leqslant i\leqslant n$
. We have
By the assumption and Lemma 4.2, for each
![]() $2\leqslant i\leqslant n$
we can write
$2\leqslant i\leqslant n$
we can write
![]() $T_{i}\!\uparrow ^{G}=S_{i1}\oplus \cdots \oplus S_{iq}$
with
$T_{i}\!\uparrow ^{G}=S_{i1}\oplus \cdots \oplus S_{iq}$
with
![]() $S_{ij}=S_{i1}\otimes _{k}Z_{j}$
for
$S_{ij}=S_{i1}\otimes _{k}Z_{j}$
for
![]() $1\leqslant j\leqslant q$
. In particular
$1\leqslant j\leqslant q$
. In particular
![]() $S_{i1}=S_{i}$
for each
$S_{i1}=S_{i}$
for each
![]() $2\leqslant i\leqslant n$
. By Theorem 3.2(b)
$2\leqslant i\leqslant n$
. By Theorem 3.2(b)

so Lemma 4.2(a) implies that

These yield that
![]() $P(S)$
has
$P(S)$
has
![]() $q$
distinct uniserial submodules
$q$
distinct uniserial submodules

Set
![]() $W=W_{1}+W_{2}+\cdots +W_{q}~\subseteq P(S)$
. Then
$W=W_{1}+W_{2}+\cdots +W_{q}~\subseteq P(S)$
. Then
![]() $\text{soc}(W)=S$
, and the Loewy and socle structure of
$\text{soc}(W)=S$
, and the Loewy and socle structure of
![]() $W$
is as follows:
$W$
is as follows:

with simple socle isomorphic to
![]() $S$
. Therefore
$S$
. Therefore
![]() $W/S$
has a proper uniserial submodule
$W/S$
has a proper uniserial submodule

Now by Corollary 3.4,
![]() $U|{\mathcal{H}}(P(S))$
, so that by Lemma 4.2(a)
$U|{\mathcal{H}}(P(S))$
, so that by Lemma 4.2(a)

for each
![]() $1\leqslant j\leqslant q$
. Therefore
$1\leqslant j\leqslant q$
. Therefore
![]() $q=2$
since
$q=2$
since
![]() ${\mathcal{H}}(P(S))$
has exactly two nonprojective indecomposable direct summands by the assumption that
${\mathcal{H}}(P(S))$
has exactly two nonprojective indecomposable direct summands by the assumption that
![]() $S$
does not lie at the end of its AR-component. Notice that this already provides a contradiction in case the characteristic of
$S$
does not lie at the end of its AR-component. Notice that this already provides a contradiction in case the characteristic of
![]() $k$
is
$k$
is
![]() $2$
, since we assume
$2$
, since we assume
![]() $q\neq p$
. So we now assume that
$q\neq p$
. So we now assume that
![]() $p\geqslant 3$
. Then, the Loewy and socle structures of PIMs
$p\geqslant 3$
. Then, the Loewy and socle structures of PIMs
![]() $P(S)$
,
$P(S)$
,
![]() $P(S_{i})$
and
$P(S_{i})$
and
![]() $P(S_{i2})$
for
$P(S_{i2})$
for
![]() $2\leqslant i\leqslant n$
are:
$2\leqslant i\leqslant n$
are:

Now considering the restrictions
![]() $S\downarrow _{N}$
and
$S\downarrow _{N}$
and
![]() $S_{i}\downarrow _{N}$
for
$S_{i}\downarrow _{N}$
for
![]() $2\leqslant i\leqslant n$
, we obtain by Lemma 4.3 that the Loewy and socle structures of the PIMs
$2\leqslant i\leqslant n$
, we obtain by Lemma 4.3 that the Loewy and socle structures of the PIMs
![]() $P(T_{1})$
,
$P(T_{1})$
,
![]() $P(T_{1}^{g})$
and
$P(T_{1}^{g})$
and
![]() $P(T_{i})$
for each
$P(T_{i})$
for each
![]() $2~\leqslant ~i~\leqslant ~n$
are
$2~\leqslant ~i~\leqslant ~n$
are

since
![]() $T_{1}\,\not \cong \,{T_{1}}^{g}$
. Now, as the dimension of any PIM for
$T_{1}\,\not \cong \,{T_{1}}^{g}$
. Now, as the dimension of any PIM for
![]() $kN$
is divisible by
$kN$
is divisible by
![]() $|N|_{p}=:p^{a}$
for an integer
$|N|_{p}=:p^{a}$
for an integer
![]() $a\geqslant 1$
, and since
$a\geqslant 1$
, and since
![]() $\dim \,T_{1}=\dim \,{T_{1}}^{g}$
, we have for each
$\dim \,T_{1}=\dim \,{T_{1}}^{g}$
, we have for each
![]() $2\leqslant i\leqslant n$
$2\leqslant i\leqslant n$
so that
This implies that
since
![]() $p\not =2$
(since
$p\not =2$
(since
![]() $q=2$
). Thus,
$q=2$
). Thus,
![]() $\dim \,T_{i}\equiv 0$
(mod
$\dim \,T_{i}\equiv 0$
(mod
![]() $p^{a}$
) for any
$p^{a}$
) for any
![]() $1\leqslant i\leqslant n$
. Now, looking at the composition factors of the PIMs
$1\leqslant i\leqslant n$
. Now, looking at the composition factors of the PIMs
![]() $P(T_{1}),P({T_{1}}^{g}),P(T_{2}),\ldots ,P(T_{n})$
, we know that
$P(T_{1}),P({T_{1}}^{g}),P(T_{2}),\ldots ,P(T_{n})$
, we know that
![]() $\text{IBr}(b)=\{T_{1},{T_{1}}^{g},T_{2},\ldots ,T_{n}\}$
, which implies that
$\text{IBr}(b)=\{T_{1},{T_{1}}^{g},T_{2},\ldots ,T_{n}\}$
, which implies that
![]() $p^{a}\,|\,\dim \,{\mathcal{T}}$
for any
$p^{a}\,|\,\dim \,{\mathcal{T}}$
for any
![]() ${\mathcal{T}}\in \text{IBr}(b)$
. Now it follows from Brauer’s result [Reference Nagao and Tsushima31, Chapter 3 Theorem 6.25] that there is a simple
${\mathcal{T}}\in \text{IBr}(b)$
. Now it follows from Brauer’s result [Reference Nagao and Tsushima31, Chapter 3 Theorem 6.25] that there is a simple
![]() ${\mathcal{T}}\in \text{IBr}(b)$
such that
${\mathcal{T}}\in \text{IBr}(b)$
such that
![]() $\unicode[STIX]{x1D708}_{p}(\dim \,{\mathcal{T}})=a-d(b)$
(where
$\unicode[STIX]{x1D708}_{p}(\dim \,{\mathcal{T}})=a-d(b)$
(where
![]() $d(b)$
is the defect of
$d(b)$
is the defect of
![]() $b$
). Hence we have a contradiction since
$b$
). Hence we have a contradiction since
![]() $b$
is a wild block, i.e., of positive defect.
$b$
is a wild block, i.e., of positive defect.
Claim 3.
(a) If there is an integer
 $2\leqslant m\leqslant n-1$
such that
$2\leqslant m\leqslant n-1$
such that
 $S_{2}\downarrow _{N},\ldots ,S_{m}\downarrow _{N}$
are not simple and
$S_{2}\downarrow _{N},\ldots ,S_{m}\downarrow _{N}$
are not simple and
 $S_{m+1}\downarrow _{N}$
is simple, then we have a contradiction.
$S_{m+1}\downarrow _{N}$
is simple, then we have a contradiction.(b) If there is an integer
 $2\leqslant m\leqslant n-1$
such that
$2\leqslant m\leqslant n-1$
such that
 $S_{2}\downarrow _{N},\ldots ,S_{m}\downarrow _{N}$
are simple and
$S_{2}\downarrow _{N},\ldots ,S_{m}\downarrow _{N}$
are simple and
 $S_{m+1}\downarrow _{N}$
is not simple, then we have a contradiction.
$S_{m+1}\downarrow _{N}$
is not simple, then we have a contradiction.
Proof of Claim 3.
(a) Set
![]() $T_{m+1}=S_{m+1}\downarrow _{N}$
. By Lemma 4.2 there exists a simple module
$T_{m+1}=S_{m+1}\downarrow _{N}$
. By Lemma 4.2 there exists a simple module
![]() $T_{m}\in \text{IBr}(b)$
with
$T_{m}\in \text{IBr}(b)$
with
![]() $S_{m}\downarrow _{N}=T_{m}\oplus {T_{m}}^{g}\oplus \cdots \oplus {T_{m}}^{g^{q-1}}$
. Then, by Lemma 4.2,
$S_{m}\downarrow _{N}=T_{m}\oplus {T_{m}}^{g}\oplus \cdots \oplus {T_{m}}^{g^{q-1}}$
. Then, by Lemma 4.2,
where
![]() $S_{m+1,j}=S_{m+1}\otimes _{k}Z_{j}$
for each
$S_{m+1,j}=S_{m+1}\otimes _{k}Z_{j}$
for each
![]() $1\leqslant j\leqslant q$
and
$1\leqslant j\leqslant q$
and
![]() $T_{m}\uparrow ^{G}=S_{m}$
. By the structure of
$T_{m}\uparrow ^{G}=S_{m}$
. By the structure of
![]() $P(S)$
, we have that
$P(S)$
, we have that
![]() $\text{Ext}_{kG}^{1}(S_{m},S_{m+1})\neq 0$
. Therefore by Eckmann–Shapiro’s lemma we have that
$\text{Ext}_{kG}^{1}(S_{m},S_{m+1})\neq 0$
. Therefore by Eckmann–Shapiro’s lemma we have that
![]() $\text{Ext}_{kN}^{1}(T_{m},T_{m+1})\neq 0$
. Thus there exists a
$\text{Ext}_{kN}^{1}(T_{m},T_{m+1})\neq 0$
. Thus there exists a
![]() $kN$
-module with Loewy structure
$kN$
-module with Loewy structure
So it follows from Lemma 2.1 that
where the right-hand side box is the Loewy and socle series. But
![]() $P(S_{m})$
is uniserial by Theorem 3.2(b), so applying again Lemma 2.1, we must have
$P(S_{m})$
is uniserial by Theorem 3.2(b), so applying again Lemma 2.1, we must have
![]() $q=1$
, which contradicts the assumption that
$q=1$
, which contradicts the assumption that
![]() $q$
is a prime.
$q$
is a prime.
(b) follows in a similar fashion using a dual argument. ◻
Altogether, Claims 1–3 prove that the simple modules
![]() $S_{2},\ldots ,S_{n}$
cannot exist, therefore
$S_{2},\ldots ,S_{n}$
cannot exist, therefore
![]() $S$
must lie at the end of its AR-component.◻
$S$
must lie at the end of its AR-component.◻
As a consequence of the above discussion we obtain Theorem B of the Introduction.
5 The principal block of
 $O^{p^{\prime }}(G)$
$O^{p^{\prime }}(G)$
From now on, we assume that
![]() $p\geqslant 3$
and
$p\geqslant 3$
and
![]() $G$
is a finite group with nontrivial abelian Sylow
$G$
is a finite group with nontrivial abelian Sylow
![]() $p$
-subgroups. Because we consider the principal block only, we assume that
$p$
-subgroups. Because we consider the principal block only, we assume that
![]() $O_{p^{\prime }}(G)=1$
since
$O_{p^{\prime }}(G)=1$
since
![]() $B_{0}(kG)\cong B_{0} (k(G/O_{p^{\prime }}(G))$
as
$B_{0}(kG)\cong B_{0} (k(G/O_{p^{\prime }}(G))$
as
![]() $k$
-algebras.
$k$
-algebras.
The structure of
![]() $O^{p^{\prime }}(G)$
can be obtained using the classification of finite simple groups and a result of Fong and Harris [Reference Fong and Harris12, 5A–5C].
$O^{p^{\prime }}(G)$
can be obtained using the classification of finite simple groups and a result of Fong and Harris [Reference Fong and Harris12, 5A–5C].
Lemma 5.1. [Reference Düvel9, Theorem 1.7]
Let
![]() $p$
be an odd prime. Let
$p$
be an odd prime. Let
![]() $G$
be a finite group with a nontrivial abelian Sylow
$G$
be a finite group with a nontrivial abelian Sylow
![]() $p$
-subgroup. Then
$p$
-subgroup. Then
where
![]() $m$
is a nonnegative integer (i.e., possibly
$m$
is a nonnegative integer (i.e., possibly
![]() $O^{p^{\prime }}(G/O_{p^{\prime }}(G))\cong Q$
),
$O^{p^{\prime }}(G/O_{p^{\prime }}(G))\cong Q$
),
![]() $Q$
is an abelian
$Q$
is an abelian
![]() $p$
-group, and for each
$p$
-group, and for each
![]() $1\leqslant i\leqslant m$
,
$1\leqslant i\leqslant m$
,
![]() $H_{i}$
is a nonabelian simple group with nontrivial Sylow
$H_{i}$
is a nonabelian simple group with nontrivial Sylow
![]() $p$
-subgroups.
$p$
-subgroups.
Therefore, we fix the notation
![]() $O^{p^{\prime }}(G)=Q\times H_{1}\times \cdots \times H_{m}$
, where
$O^{p^{\prime }}(G)=Q\times H_{1}\times \cdots \times H_{m}$
, where
![]() $Q$
is an abelian
$Q$
is an abelian
![]() $p$
-group, and
$p$
-group, and
![]() $H_{1},\ldots ,H_{m}$
are nonabelian simple groups with nontrivial Sylow
$H_{1},\ldots ,H_{m}$
are nonabelian simple groups with nontrivial Sylow
![]() $p$
-subgroups as given by Lemma 5.1.
$p$
-subgroups as given by Lemma 5.1.
5.1 Simple modules in infinite tubes
 $\mathbb{Z}A_{\infty }/\langle \unicode[STIX]{x1D70F}^{a}\rangle$
$\mathbb{Z}A_{\infty }/\langle \unicode[STIX]{x1D70F}^{a}\rangle$
Lemma 5.2. ([Reference Kawata, Michler and Uno21, Lemma 5.2] generalized version)
Let
![]() $H=\tilde{H}_{1}\times \cdots \times \tilde{H}_{m}~(m\geqslant 1)$
be a finite group such that
$H=\tilde{H}_{1}\times \cdots \times \tilde{H}_{m}~(m\geqslant 1)$
be a finite group such that
![]() $p\mid |\tilde{H}_{i}|$
for each
$p\mid |\tilde{H}_{i}|$
for each
![]() $1\leqslant i\leqslant m$
. If
$1\leqslant i\leqslant m$
. If
![]() $B_{0}(kH)$
is a wild block and contains a periodic simple module, then
$B_{0}(kH)$
is a wild block and contains a periodic simple module, then
![]() $m=1$
.
$m=1$
.
Proof. Let
![]() $S$
be a simple periodic
$S$
be a simple periodic
![]() $B_{0}(kH)$
-module. Then we may write
$B_{0}(kH)$
-module. Then we may write
![]() $S=S_{1}\otimes _{k}\cdots \otimes _{k}\,S_{m}$
where
$S=S_{1}\otimes _{k}\cdots \otimes _{k}\,S_{m}$
where
![]() $S_{i}$
is a simple
$S_{i}$
is a simple
![]() $B_{0}(k\tilde{H}_{i})$
-module for each
$B_{0}(k\tilde{H}_{i})$
-module for each
![]() $1\leqslant i\leqslant m$
. Then, by iterating [Reference Kawata, Michler and Uno21, Lemma 2.2], there exists an index
$1\leqslant i\leqslant m$
. Then, by iterating [Reference Kawata, Michler and Uno21, Lemma 2.2], there exists an index
![]() $1\leqslant i_{0}\leqslant m$
such that
$1\leqslant i_{0}\leqslant m$
such that
![]() $S_{i_{0}}$
is periodic and
$S_{i_{0}}$
is periodic and
![]() $S_{j}$
is a projective
$S_{j}$
is a projective
![]() $k\tilde{H}_{j}$
-module for each
$k\tilde{H}_{j}$
-module for each
![]() $1\leqslant j\neq i_{0}\leqslant m$
. But
$1\leqslant j\neq i_{0}\leqslant m$
. But
![]() $B_{0}(k\tilde{H}_{j})$
cannot contain a simple projective module, since we assume that
$B_{0}(k\tilde{H}_{j})$
cannot contain a simple projective module, since we assume that
![]() $p\mid |\tilde{H}_{i}|$
for each
$p\mid |\tilde{H}_{i}|$
for each
![]() $1\leqslant i\leqslant m$
. Hence this forces
$1\leqslant i\leqslant m$
. Hence this forces
![]() $H=\tilde{H}_{i_{0}}$
, i.e.,
$H=\tilde{H}_{i_{0}}$
, i.e.,
![]() $m=1$
.◻
$m=1$
.◻
As a consequence, the existence of simple periodic modules in the principal block lying in tubes drastically restricts the possible structure of
![]() $O^{p^{\prime }}(G)$
.
$O^{p^{\prime }}(G)$
.
Corollary 5.3. If
![]() $B_{0}(kG)$
contains a periodic simple module, then
$B_{0}(kG)$
contains a periodic simple module, then
![]() $O^{p^{\prime }}(G)=H_{1}$
is a nonabelian finite simple group with noncyclic abelian Sylow
$O^{p^{\prime }}(G)=H_{1}$
is a nonabelian finite simple group with noncyclic abelian Sylow
![]() $p$
-subgroups.
$p$
-subgroups.
Proof. By Lemma 5.2, either
![]() $O^{p^{\prime }}(G)=Q$
or
$O^{p^{\prime }}(G)=Q$
or
![]() $O^{p^{\prime }}(G)=H_{1}$
. But the former cannot happen. Indeed, the indecomposable direct summands of the restriction to
$O^{p^{\prime }}(G)=H_{1}$
. But the former cannot happen. Indeed, the indecomposable direct summands of the restriction to
![]() $O^{p^{\prime }}(G)$
of a simple periodic
$O^{p^{\prime }}(G)$
of a simple periodic
![]() $kG$
-module are all simple periodic modules, however the unique simple
$kG$
-module are all simple periodic modules, however the unique simple
![]() $kQ$
-module is the trivial module, which is not periodic since we assume that
$kQ$
-module is the trivial module, which is not periodic since we assume that
![]() $B_{0}(kG)$
is wild, and hence
$B_{0}(kG)$
is wild, and hence
![]() $Q$
is noncyclic. This leaves only the possibility
$Q$
is noncyclic. This leaves only the possibility
![]() $O^{p^{\prime }}(G)=H_{1}$
, and the
$O^{p^{\prime }}(G)=H_{1}$
, and the
![]() $p$
-rank of
$p$
-rank of
![]() $H_{1}$
must be at least
$H_{1}$
must be at least
![]() $2$
again because we assume that
$2$
again because we assume that
![]() $B_{0}(kG)$
is wild.◻
$B_{0}(kG)$
is wild.◻
This immediately leads to the following reduction to nonabelian simple groups:
Corollary 5.4. Assume that every periodic simple
![]() $B_{0}(kH)$
-module lies at the end of its AR-component for every nonabelian finite simple group
$B_{0}(kH)$
-module lies at the end of its AR-component for every nonabelian finite simple group
![]() $H$
with noncyclic abelian Sylow
$H$
with noncyclic abelian Sylow
![]() $p$
-subgroups. Then every simple periodic
$p$
-subgroups. Then every simple periodic
![]() $B_{0}(kO^{p^{\prime }}(G))$
-module lies at the end of its AR-component for any finite group
$B_{0}(kO^{p^{\prime }}(G))$
-module lies at the end of its AR-component for any finite group
![]() $G$
with
$G$
with
![]() $O_{p^{\prime }}(G)=1$
and noncyclic abelian Sylow
$O_{p^{\prime }}(G)=1$
and noncyclic abelian Sylow
![]() $p$
-subgroups.
$p$
-subgroups.
5.2 Simple modules in
 $\mathbb{Z}A_{\infty }$
-components
$\mathbb{Z}A_{\infty }$
-components
Lemma 5.5. Let
![]() $H=\tilde{H}_{1}\times \cdots \times \tilde{H}_{m}~(m\geqslant 1)$
be a finite group with abelian Sylow
$H=\tilde{H}_{1}\times \cdots \times \tilde{H}_{m}~(m\geqslant 1)$
be a finite group with abelian Sylow
![]() $p$
-subgroups such that
$p$
-subgroups such that
![]() $p\mid |\tilde{H}_{i}|$
for each
$p\mid |\tilde{H}_{i}|$
for each
![]() $1\leqslant i\leqslant m$
. If
$1\leqslant i\leqslant m$
. If
![]() $B_{0}(kH)$
is a wild block containing a nonperiodic simple module
$B_{0}(kH)$
is a wild block containing a nonperiodic simple module
![]() $S$
not lying at the end of its AR-component, then
$S$
not lying at the end of its AR-component, then
![]() $m=1$
.
$m=1$
.
This lemma and its proof below generalize parts of the proof of [Reference Kawata, Michler and Uno21, Theorem 5(i)].
Proof. Assume that
![]() $m\geqslant 2$
. Then by Theorem 3.2(b), there exists a simple
$m\geqslant 2$
. Then by Theorem 3.2(b), there exists a simple
![]() $B_{0}(kH)$
-module
$B_{0}(kH)$
-module
![]() $T$
lying at the end of
$T$
lying at the end of
![]() $\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
. By Knörr’s Theorem [Reference Knörr23, 3.7 Corollary], we know that the vertices of the simple modules in
$\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
. By Knörr’s Theorem [Reference Knörr23, 3.7 Corollary], we know that the vertices of the simple modules in
![]() $B_{0}(kH)$
are the Sylow
$B_{0}(kH)$
are the Sylow
![]() $p$
-subgroups of
$p$
-subgroups of
![]() $H$
, because they are abelian. Now by assumption
$H$
, because they are abelian. Now by assumption
![]() $\unicode[STIX]{x1D6E4}_{s}(S)\cong \mathbb{Z}A_{\infty }$
by [Reference Erdmann11], which implies that all the modules in
$\unicode[STIX]{x1D6E4}_{s}(S)\cong \mathbb{Z}A_{\infty }$
by [Reference Erdmann11], which implies that all the modules in
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
and
$\unicode[STIX]{x1D6E4}_{s}(S)$
and
![]() $\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
have the Sylow
$\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
have the Sylow
![]() $p$
-subgroups as their vertices by [Reference Okuyama and Uno32, Theorem]. So all the modules in
$p$
-subgroups as their vertices by [Reference Okuyama and Uno32, Theorem]. So all the modules in
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
and
$\unicode[STIX]{x1D6E4}_{s}(S)$
and
![]() $\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
are not projective relatively to the subgroup
$\unicode[STIX]{x1D6E4}_{s}(\unicode[STIX]{x1D6FA}(S))$
are not projective relatively to the subgroup
![]() $N=\tilde{H}_{1}\times \cdots \times \tilde{H}_{m-1}$
as it does not contain a Sylow
$N=\tilde{H}_{1}\times \cdots \times \tilde{H}_{m-1}$
as it does not contain a Sylow
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $H$
. Thus, as
$H$
. Thus, as
![]() $p\neq 2$
, all the simple direct summands of
$p\neq 2$
, all the simple direct summands of
![]() $S\downarrow _{N}$
belong to blocks of defect zero by [Reference Kawata, Michler and Uno21, Lemma 1.4]. But
$S\downarrow _{N}$
belong to blocks of defect zero by [Reference Kawata, Michler and Uno21, Lemma 1.4]. But
and hence there exist a simple
![]() $B_{0}(kN)$
-module
$B_{0}(kN)$
-module
![]() $S_{0}$
and a simple
$S_{0}$
and a simple
![]() $B_{0}(k\tilde{H}_{m})$
-module
$B_{0}(k\tilde{H}_{m})$
-module
![]() $S_{m}$
such that
$S_{m}$
such that
Because
![]() $S\downarrow _{N}\cong (\dim _{k}S_{m})S_{0}$
, the module
$S\downarrow _{N}\cong (\dim _{k}S_{m})S_{0}$
, the module
![]() $S_{0}$
is a projective
$S_{0}$
is a projective
![]() $kN$
-module by the above. Hence by Lemma 2.3
$kN$
-module by the above. Hence by Lemma 2.3
![]() $S$
is relatively
$S$
is relatively
![]() $\tilde{H}_{m}$
-projective. This contradicts the fact that the vertices of
$\tilde{H}_{m}$
-projective. This contradicts the fact that the vertices of
![]() $S$
are the Sylow
$S$
are the Sylow
![]() $p$
-subgroups of
$p$
-subgroups of
![]() $H$
. Thus we conclude that
$H$
. Thus we conclude that
![]() $S$
must lie at the end of
$S$
must lie at the end of
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
.◻
$\unicode[STIX]{x1D6E4}_{s}(S)$
.◻
Proposition 5.6. Let
![]() $G$
be a finite group with
$G$
be a finite group with
![]() $O_{p^{\prime }}(G)=1$
and noncyclic abelian Sylow
$O_{p^{\prime }}(G)=1$
and noncyclic abelian Sylow
![]() $p$
-subgroups. Assume moreover that one of Conditions (i), (ii), or (iii) of Theorem C is satisfied. Then every nonperiodic simple
$p$
-subgroups. Assume moreover that one of Conditions (i), (ii), or (iii) of Theorem C is satisfied. Then every nonperiodic simple
![]() $B_{0}(kO^{p^{\prime }}(G))$
-module lies at the end of its AR-component.
$B_{0}(kO^{p^{\prime }}(G))$
-module lies at the end of its AR-component.
Proof. We have
![]() $O^{p^{\prime }}(G)=Q$
or
$O^{p^{\prime }}(G)=Q$
or
![]() $O^{p^{\prime }}(G)=Q\times H_{1}\times \cdots \times H_{m}$
, where
$O^{p^{\prime }}(G)=Q\times H_{1}\times \cdots \times H_{m}$
, where
![]() $Q$
is an abelian
$Q$
is an abelian
![]() $p$
-group and
$p$
-group and
![]() $H_{i}$
is a nonabelian finite simple group with nontrivial Sylow
$H_{i}$
is a nonabelian finite simple group with nontrivial Sylow
![]() $p$
-subgroups for each
$p$
-subgroups for each
![]() $1\leqslant i\leqslant m$
.
$1\leqslant i\leqslant m$
.
If (i) holds, that is
![]() $Q\neq 1$
, then by Theorem 3.1(a), all simple
$Q\neq 1$
, then by Theorem 3.1(a), all simple
![]() $B_{0}(kO^{p^{\prime }}(G))$
-modules lie at the end of their AR-components. Therefore, we assume for the rest of the proof that
$B_{0}(kO^{p^{\prime }}(G))$
-modules lie at the end of their AR-components. Therefore, we assume for the rest of the proof that
![]() $Q=1$
.
$Q=1$
.
Next if (ii) holds, that is
![]() $m\geqslant 2$
, the claim follows from Lemma 5.5.
$m\geqslant 2$
, the claim follows from Lemma 5.5.
Finally if (iii) holds, that is
![]() $O^{p^{\prime }}(G)=H_{1}$
, then
$O^{p^{\prime }}(G)=H_{1}$
, then
![]() $H_{1}$
must have a noncyclic Sylow
$H_{1}$
must have a noncyclic Sylow
![]() $p$
-subgroup, therefore all simple
$p$
-subgroup, therefore all simple
![]() $B_{0}(kO^{p^{\prime }}(G))$
-modules lie at the end of their
$B_{0}(kO^{p^{\prime }}(G))$
-modules lie at the end of their
![]() $AR$
-components by assumption.◻
$AR$
-components by assumption.◻
6 Reduction to
 $O^{p^{\prime }}(G)$
$O^{p^{\prime }}(G)$
We continue assuming that
![]() $G$
is a finite group with noncyclic abelian Sylow
$G$
is a finite group with noncyclic abelian Sylow
![]() $p$
-subgroups such that
$p$
-subgroups such that
![]() $O_{p^{\prime }}(G)=1$
, unless otherwise stated. We now prove that an answer to Question A is detected by restriction to the normal subgroup
$O_{p^{\prime }}(G)=1$
, unless otherwise stated. We now prove that an answer to Question A is detected by restriction to the normal subgroup
![]() $O^{p^{\prime }}(G)$
of
$O^{p^{\prime }}(G)$
of
![]() $G$
.
$G$
.
We set
![]() $H=O^{p^{\prime }}(G)$
, let
$H=O^{p^{\prime }}(G)$
, let
![]() $P\in \text{Syl}_{p}(H)$
be a Sylow
$P\in \text{Syl}_{p}(H)$
be a Sylow
![]() $p$
-subgroup, and set
$p$
-subgroup, and set
![]() $N=HC_{G}(P)$
. Moreover we set
$N=HC_{G}(P)$
. Moreover we set
![]() $B=B_{0}(kG)$
,
$B=B_{0}(kG)$
,
![]() $b=B_{0}(kN)$
and
$b=B_{0}(kN)$
and
![]() $\tilde{b}=B_{0}(kH)$
. Then
$\tilde{b}=B_{0}(kH)$
. Then
![]() $N$
is Dade’s Group
$N$
is Dade’s Group
![]() $G[\tilde{b}]$
and
$G[\tilde{b}]$
and
![]() $N\unlhd G$
, see Lemma 2.2.
$N\unlhd G$
, see Lemma 2.2.
First of all Question A has an affirmative answer for the group
![]() $N$
if and only if it has an affirmative answer for the group
$N$
if and only if it has an affirmative answer for the group
![]() $H$
.
$H$
.
Lemma 6.1. With the above notation, every simple
![]() $b$
-module lies at the end of its AR-component if and only if every simple
$b$
-module lies at the end of its AR-component if and only if every simple
![]() $\tilde{b}$
-module lies at the end of its AR-component.
$\tilde{b}$
-module lies at the end of its AR-component.
Proof. By the Alperin–Dade theorem [Reference Dade8, Theorem] (see [Reference Alperin1]), the blocks
![]() $b$
and
$b$
and
![]() $\tilde{b}$
are isomorphic as
$\tilde{b}$
are isomorphic as
![]() $k$
-algebras, hence Morita equivalent. But for a simple module, lying at the end of its AR-component is a property preserved by Morita equivalence.◻
$k$
-algebras, hence Morita equivalent. But for a simple module, lying at the end of its AR-component is a property preserved by Morita equivalence.◻
Proposition 6.2. If every simple
![]() $\tilde{b}$
-module lies at the end of its AR-component, then every simple
$\tilde{b}$
-module lies at the end of its AR-component, then every simple
![]() $B$
-module lies at the end of its AR-component.
$B$
-module lies at the end of its AR-component.
Proof. Let
![]() $S$
be a simple
$S$
be a simple
![]() $B$
-module and let
$B$
-module and let
![]() $T$
be a simple direct summand of
$T$
be a simple direct summand of
![]() $S\downarrow _{H}$
. Then
$S\downarrow _{H}$
. Then
![]() $T$
is periodic if and only if
$T$
is periodic if and only if
![]() $S$
is. Therefore
$S$
is. Therefore
![]() $\unicode[STIX]{x1D6E4}_{s}(S)\cong \mathbb{Z}A_{\infty }$
if and only if
$\unicode[STIX]{x1D6E4}_{s}(S)\cong \mathbb{Z}A_{\infty }$
if and only if
![]() $\unicode[STIX]{x1D6E4}_{s}(T)~\cong ~\mathbb{Z}A_{\infty }$
, and
$\unicode[STIX]{x1D6E4}_{s}(T)~\cong ~\mathbb{Z}A_{\infty }$
, and
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
is an infinite tube with tree class
$\unicode[STIX]{x1D6E4}_{s}(S)$
is an infinite tube with tree class
![]() $A_{\infty }$
if and only if
$A_{\infty }$
if and only if
![]() $\unicode[STIX]{x1D6E4}_{s}(T)$
is an infinite tube with tree class
$\unicode[STIX]{x1D6E4}_{s}(T)$
is an infinite tube with tree class
![]() $A_{\infty }$
.
$A_{\infty }$
.
In case
![]() $\unicode[STIX]{x1D6E4}_{s}(S)\cong \mathbb{Z}A_{\infty }$
, then
$\unicode[STIX]{x1D6E4}_{s}(S)\cong \mathbb{Z}A_{\infty }$
, then
![]() $S$
lies at the end of
$S$
lies at the end of
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
if and only if
$\unicode[STIX]{x1D6E4}_{s}(S)$
if and only if
![]() $T$
lies at the end of
$T$
lies at the end of
![]() $\unicode[STIX]{x1D6E4}_{s}(T)$
by [Reference Kawata, Michler and Uno21, Lemma 1.5].
$\unicode[STIX]{x1D6E4}_{s}(T)$
by [Reference Kawata, Michler and Uno21, Lemma 1.5].
In case
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
is an infinite tube with tree class
$\unicode[STIX]{x1D6E4}_{s}(S)$
is an infinite tube with tree class
![]() $A_{\infty }$
, then by Corollary 5.3,
$A_{\infty }$
, then by Corollary 5.3,
![]() $H$
is a nonabelian finite simple group with noncyclic abelian Sylow
$H$
is a nonabelian finite simple group with noncyclic abelian Sylow
![]() $p$
-subgroups. Now, by Schreier’s conjecture (now proven by the Classification of Finite Simple Groups, see [Reference Gorenstein, Lyons and Solomon15, Definition 2.1] and [Reference Gorenstein, Lyons and Solomon16, Theorem 7.1.1]), we know that
$p$
-subgroups. Now, by Schreier’s conjecture (now proven by the Classification of Finite Simple Groups, see [Reference Gorenstein, Lyons and Solomon15, Definition 2.1] and [Reference Gorenstein, Lyons and Solomon16, Theorem 7.1.1]), we know that
![]() $G/H$
is a solvable
$G/H$
is a solvable
![]() $p^{\prime }$
-subgroup of
$p^{\prime }$
-subgroup of
![]() $\text{Out}(H)$
. Now by Lemma 6.1, we may assume
$\text{Out}(H)$
. Now by Lemma 6.1, we may assume
![]() $H=N$
and by Lemma 2.2(c) we have
$H=N$
and by Lemma 2.2(c) we have
![]() $1_{B}=1_{b}$
. Therefore Theorem B implies that
$1_{B}=1_{b}$
. Therefore Theorem B implies that
![]() $S$
lies at the end of
$S$
lies at the end of
![]() $\unicode[STIX]{x1D6E4}_{s}(S)$
because every simple
$\unicode[STIX]{x1D6E4}_{s}(S)$
because every simple
![]() $b$
-module lies at the end of its AR-component.◻
$b$
-module lies at the end of its AR-component.◻
As a corollary, we obtain Theorem C of the Introduction.
Proof of Theorem C.
Let
![]() $G$
be a finite group with noncyclic abelian Sylow
$G$
be a finite group with noncyclic abelian Sylow
![]() $p$
-subgroups. As
$p$
-subgroups. As
![]() $B_{0}(kG)\cong B_{0}(k\,G/O_{p^{\prime }}(G))$
as
$B_{0}(kG)\cong B_{0}(k\,G/O_{p^{\prime }}(G))$
as
![]() $k$
-algebras, we may assume that
$k$
-algebras, we may assume that
![]() $O_{p^{\prime }}(G)=1$
. Therefore, by Proposition 6.2, every simple
$O_{p^{\prime }}(G)=1$
. Therefore, by Proposition 6.2, every simple
![]() $B_{0}(kG)$
-module lies at the end of its AR-component if every simple
$B_{0}(kG)$
-module lies at the end of its AR-component if every simple
![]() $B_{0}(k\,O^{p^{\prime }}(G))$
-module lies at the end of its AR-component. Now if
$B_{0}(k\,O^{p^{\prime }}(G))$
-module lies at the end of its AR-component. Now if
![]() $B_{0}(kG)$
contains a periodic simple module, then by Corollary 5.3 we must have that
$B_{0}(kG)$
contains a periodic simple module, then by Corollary 5.3 we must have that
![]() $O^{p^{\prime }}(G)=H_{1}$
is a nonabelian finite simple group with noncyclic abelian Sylow
$O^{p^{\prime }}(G)=H_{1}$
is a nonabelian finite simple group with noncyclic abelian Sylow
![]() $p$
-subgroups, then the claim holds by Corollary 5.4. Therefore we may assume that
$p$
-subgroups, then the claim holds by Corollary 5.4. Therefore we may assume that
![]() $B_{0}(kG)$
, and hence
$B_{0}(kG)$
, and hence
![]() $B_{0}(k\,O^{p^{\prime }}(G))$
, contains no periodic simple module. In this case, if one of Conditions (i), (ii), or (iii) holds, then the claim follows from Proposition 5.6.◻
$B_{0}(k\,O^{p^{\prime }}(G))$
, contains no periodic simple module. In this case, if one of Conditions (i), (ii), or (iii) holds, then the claim follows from Proposition 5.6.◻
7 Principal
 $3$
-blocks
$3$
-blocks
We now fix
![]() $p=3$
, and continue assuming that
$p=3$
, and continue assuming that
![]() $G$
is a finite group with noncyclic Sylow
$G$
is a finite group with noncyclic Sylow
![]() $3$
-subgroups, so that
$3$
-subgroups, so that
![]() $B_{0}(kG)$
is wild. We may also assume that
$B_{0}(kG)$
is wild. We may also assume that
![]() $O_{3^{\prime }}(G)=1$
.
$O_{3^{\prime }}(G)=1$
.
We start by investigating principal
![]() $3$
-blocks of nonabelian finite simple groups with abelian defect group. To this aim, we recall that the list of nonabelian finite simple groups with abelian Sylow
$3$
-blocks of nonabelian finite simple groups with abelian defect group. To this aim, we recall that the list of nonabelian finite simple groups with abelian Sylow
![]() $3$
-subgroups is known by the classification of finite simple groups and was determined by Paul Fong (in an unpublished manuscript).
$3$
-subgroups is known by the classification of finite simple groups and was determined by Paul Fong (in an unpublished manuscript).
Proposition 7.1. [Reference Koshitani and Yoshii25, Proposition 4.3]
If
![]() $G$
is a nonabelian finite simple group with noncyclic abelian Sylow
$G$
is a nonabelian finite simple group with noncyclic abelian Sylow
![]() $3$
-subgroup, then
$3$
-subgroup, then
![]() $G$
is one of:
$G$
is one of:
(i)
 $\mathfrak{A}_{7}$
,
$\mathfrak{A}_{7}$
,
 $\mathfrak{A}_{8}$
,
$\mathfrak{A}_{8}$
,
 $M_{11}$
,
$M_{11}$
,
 $M_{22}$
,
$M_{22}$
,
 $M_{23}$
,
$M_{23}$
,
 $HS$
,
$HS$
,
 $O^{\prime }N$
;
$O^{\prime }N$
;(ii)
 $\text{PSL}_{3}(q)$
for a prime power
$\text{PSL}_{3}(q)$
for a prime power
 $q$
such that
$q$
such that
 $3||(q-1)$
;
$3||(q-1)$
;(iii)
 $\text{PSU}_{3}(q^{2})$
for a prime power
$\text{PSU}_{3}(q^{2})$
for a prime power
 $q$
such that
$q$
such that
 $3||(q+1)$
;
$3||(q+1)$
;(iv)
 $\text{PSp}_{4}(q)$
for a prime power
$\text{PSp}_{4}(q)$
for a prime power
 $q$
such that
$q$
such that
 $3|(q-1)$
;
$3|(q-1)$
;(v)
 $\text{PSp}_{4}(q)$
for a prime power
$\text{PSp}_{4}(q)$
for a prime power
 $q$
such that
$q$
such that
 $q>2$
and
$q>2$
and
 $3|(q+1)$
;
$3|(q+1)$
;(vi)
 $\text{PSL}_{4}(q)$
for a prime power
$\text{PSL}_{4}(q)$
for a prime power
 $q$
such that
$q$
such that
 $q>2$
and
$q>2$
and
 $3|(q+1)$
;
$3|(q+1)$
;(vii)
 $\text{PSU}_{4}(q^{2})$
for a prime power
$\text{PSU}_{4}(q^{2})$
for a prime power
 $q$
such that
$q$
such that
 $3|(q-1)$
;
$3|(q-1)$
;(viii)
 $\text{PSL}_{5}(q)$
for a prime power
$\text{PSL}_{5}(q)$
for a prime power
 $q$
such that
$q$
such that
 $3|(q+1)$
;
$3|(q+1)$
;(ix)
 $\text{PSU}_{5}(q^{2})$
for a prime power
$\text{PSU}_{5}(q^{2})$
for a prime power
 $q$
such that
$q$
such that
 $3|(q-1)$
; or
$3|(q-1)$
; or(x)
 $\text{PSL}_{2}(3^{n})$
for an integer
$\text{PSL}_{2}(3^{n})$
for an integer
 $n\geqslant 2$
.
$n\geqslant 2$
.
As a consequence we obtain:
Proposition 7.2. If
![]() $G$
is a nonabelian finite simple group with noncyclic abelian Sylow
$G$
is a nonabelian finite simple group with noncyclic abelian Sylow
![]() $3$
-subgroups, then every simple
$3$
-subgroups, then every simple
![]() $B_{0}(kG)$
-modules lies at the end of its component in
$B_{0}(kG)$
-modules lies at the end of its component in
![]() $\unicode[STIX]{x1D6E4}_{s}(B_{0}(kG))$
.
$\unicode[STIX]{x1D6E4}_{s}(B_{0}(kG))$
.
Proof. Let
![]() $P\in \text{Syl}_{3}(G)$
, and set
$P\in \text{Syl}_{3}(G)$
, and set
![]() $N=N_{G}(P)$
and
$N=N_{G}(P)$
and
![]() $B_{0}=B_{0}(kG)$
. We go through the list of groups in Proposition 7.1.
$B_{0}=B_{0}(kG)$
. We go through the list of groups in Proposition 7.1.
In case (i), in all cases all simple
![]() $B_{0}$
-modules lie at the end of their component in
$B_{0}$
-modules lie at the end of their component in
![]() $\unicode[STIX]{x1D6E4}_{s}(B_{0})$
by Theorem 3.2(b): indeed if
$\unicode[STIX]{x1D6E4}_{s}(B_{0})$
by Theorem 3.2(b): indeed if
![]() $G$
is one of
$G$
is one of
![]() $\mathfrak{A}_{8}$
,
$\mathfrak{A}_{8}$
,
![]() $M_{22}$
or
$M_{22}$
or
![]() $O^{\prime }N$
, then one checks from GAP [14] that the Cartan matrix of
$O^{\prime }N$
, then one checks from GAP [14] that the Cartan matrix of
![]() $B_{0}$
has no diagonal entry equal to
$B_{0}$
has no diagonal entry equal to
![]() $2$
. If
$2$
. If
![]() $G$
is one of
$G$
is one of
![]() $\mathfrak{A}_{7}$
,
$\mathfrak{A}_{7}$
,
![]() $M_{11}$
,
$M_{11}$
,
![]() $M_{23}$
, or
$M_{23}$
, or
![]() $HS$
, then one checks from GAP [14] that the Cartan matrix of
$HS$
, then one checks from GAP [14] that the Cartan matrix of
![]() $B_{0}$
does not have the shape of Theorem 3.2(b) either.
$B_{0}$
does not have the shape of Theorem 3.2(b) either.
In case (ii), then the Cartan matrix of
![]() $B_{0}$
is computed in [Reference Kunugi28, Table 2] and does not satisfy Theorem 3.2(b).
$B_{0}$
is computed in [Reference Kunugi28, Table 2] and does not satisfy Theorem 3.2(b).
Next if
![]() $G$
is one of the groups listed in Proposition 7.1(iii), (iv), (vii), or (ix), then it is proven in [Reference Koshitani and Yoshii25, Lemma 3.7] that
$G$
is one of the groups listed in Proposition 7.1(iii), (iv), (vii), or (ix), then it is proven in [Reference Koshitani and Yoshii25, Lemma 3.7] that
![]() $B_{0}$
is Puig equivalent to
$B_{0}$
is Puig equivalent to
![]() $B_{0}(kN)$
. But
$B_{0}(kN)$
. But
![]() $N$
has a nontrivial normal Sylow
$N$
has a nontrivial normal Sylow
![]() $3$
-subgroup, therefore all simple
$3$
-subgroup, therefore all simple
![]() $B_{0}(kN)$
-modules lie at the end of their components in
$B_{0}(kN)$
-modules lie at the end of their components in
![]() $\unicode[STIX]{x1D6E4}_{s}(B_{0}(kN))$
by Theorem 3.1(a), and therefore so do the simple
$\unicode[STIX]{x1D6E4}_{s}(B_{0}(kN))$
by Theorem 3.1(a), and therefore so do the simple
![]() $B_{0}$
-modules via the latter Puig (Morita) equivalence.
$B_{0}$
-modules via the latter Puig (Morita) equivalence.
In case (v), the decomposition numbers of
![]() $B_{0}$
were computed by White and Okuyama–Waki. If
$B_{0}$
were computed by White and Okuyama–Waki. If
![]() $q$
is even then we read from [Reference White36, Table II] that each column of the decomposition matrix of
$q$
is even then we read from [Reference White36, Table II] that each column of the decomposition matrix of
![]() $B_{0}$
has at least
$B_{0}$
has at least
![]() $3$
positive entries. If
$3$
positive entries. If
![]() $q$
is odd, then the decomposition matrix of
$q$
is odd, then the decomposition matrix of
![]() $B_{0}$
is given in [Reference White35, Theorem 4.2] up to two parameters
$B_{0}$
is given in [Reference White35, Theorem 4.2] up to two parameters
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. But [Reference Okuyama and Waki33, Theorem 2.3] proves that
$\unicode[STIX]{x1D6FD}$
. But [Reference Okuyama and Waki33, Theorem 2.3] proves that
![]() $\unicode[STIX]{x1D6FC}\in \{1,2\}$
. This is enough to see that each column of the decomposition matrix of
$\unicode[STIX]{x1D6FC}\in \{1,2\}$
. This is enough to see that each column of the decomposition matrix of
![]() $B_{0}$
has at least
$B_{0}$
has at least
![]() $3$
positive entries. Therefore in both cases all the diagonal entries of the Cartan matrix of
$3$
positive entries. Therefore in both cases all the diagonal entries of the Cartan matrix of
![]() $B_{0}$
are at least
$B_{0}$
are at least
![]() $3$
.
$3$
.
In cases (vi) and (viii), we proceed as follows. For
![]() $n\in \{4,5\}$
fixed, we may regard
$n\in \{4,5\}$
fixed, we may regard
![]() $B_{0}(k\text{PSL}_{n}(q))$
as the principal block of
$B_{0}(k\text{PSL}_{n}(q))$
as the principal block of
![]() $\text{SL}_{n}(q)$
as
$\text{SL}_{n}(q)$
as
![]() $3\nmid |Z(\text{SL}_{n}(q))|$
. Then we check that the Cartan matrix of
$3\nmid |Z(\text{SL}_{n}(q))|$
. Then we check that the Cartan matrix of
![]() $B_{0}(k\text{GL}_{n}(q))$
does not satisfy Theorem 3.2(b). To this end we use the information on the decomposition numbers of
$B_{0}(k\text{GL}_{n}(q))$
does not satisfy Theorem 3.2(b). To this end we use the information on the decomposition numbers of
![]() $B_{0}(k\text{GL}_{n}(q))$
provided in [Reference James19, Appendix I]. In both cases, it is enough to consider only the square submatrix
$B_{0}(k\text{GL}_{n}(q))$
provided in [Reference James19, Appendix I]. In both cases, it is enough to consider only the square submatrix
![]() $\unicode[STIX]{x1D6E5}_{n,0}$
of the decomposition matrix of
$\unicode[STIX]{x1D6E5}_{n,0}$
of the decomposition matrix of
![]() $B_{0}(k\text{GL}_{n}(q))$
whose rows are indexed by the unipotent characters. Both in case
$B_{0}(k\text{GL}_{n}(q))$
whose rows are indexed by the unipotent characters. Both in case
![]() $n=4$
and
$n=4$
and
![]() $n=5$
, there are five modular characters in the principal block (using [Reference Fong and Srinivasan13]) and
$n=5$
, there are five modular characters in the principal block (using [Reference Fong and Srinivasan13]) and
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{4,0}=\left[\begin{array}{@{}ccccccc@{}}(4) & & 1 & & & & \\ (31) & & 1 & 1 & & & \\ (2^{2}) & & & 1 & 1 & & \\ (21^{2}) & & 1 & 1 & 1 & 1 & \\ (1^{4}) & & 1 & & & 1 & 1\end{array}\right]\qquad \unicode[STIX]{x1D6E5}_{5,0}=\left[\begin{array}{@{}ccccccc@{}}(5) & & 1 & & & & \\ (32) & & & 1 & & & \\ (31^{2}) & & 1 & 1 & 1 & & \\ (2^{2}1) & & & 1 & 1 & 1 & \\ (1^{5}) & & 1 & & 1 & & 1\end{array}\right]\!.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{4,0}=\left[\begin{array}{@{}ccccccc@{}}(4) & & 1 & & & & \\ (31) & & 1 & 1 & & & \\ (2^{2}) & & & 1 & 1 & & \\ (21^{2}) & & 1 & 1 & 1 & 1 & \\ (1^{4}) & & 1 & & & 1 & 1\end{array}\right]\qquad \unicode[STIX]{x1D6E5}_{5,0}=\left[\begin{array}{@{}ccccccc@{}}(5) & & 1 & & & & \\ (32) & & & 1 & & & \\ (31^{2}) & & 1 & 1 & 1 & & \\ (2^{2}1) & & & 1 & 1 & 1 & \\ (1^{5}) & & 1 & & 1 & & 1\end{array}\right]\!.\end{eqnarray}$$
(See e.g., [Reference Koshitani and Miyachi24, Propositions 3.1 and 4.1].) It follows that the Cartan integers of
![]() $B_{0}(\text{GL}_{n}(q))$
have lower bounds given by the entries of the following matrices:
$B_{0}(\text{GL}_{n}(q))$
have lower bounds given by the entries of the following matrices:
 $$\begin{eqnarray}^{T}\!\unicode[STIX]{x1D6E5}_{4,0}\unicode[STIX]{x1D6E5}_{4,0}=\left[\begin{array}{@{}ccccc@{}}4 & 2 & 1 & 2 & 1\\ 2 & 3 & 2 & 1 & 0\\ 1 & 2 & 2 & 1 & 0\\ 2 & 1 & 1 & 2 & 1\\ 1 & 0 & 0 & 1 & 1\end{array}\right]\qquad ^{T}\!\unicode[STIX]{x1D6E5}_{5,0}\unicode[STIX]{x1D6E5}_{5,0}=\left[\begin{array}{@{}ccccc@{}}3 & 1 & 2 & 0 & 1\\ 1 & 3 & 2 & 1 & 0\\ 2 & 2 & 3 & 1 & 1\\ 0 & 1 & 1 & 1 & 0\\ 1 & 0 & 1 & 0 & 1\end{array}\right]\end{eqnarray}$$
$$\begin{eqnarray}^{T}\!\unicode[STIX]{x1D6E5}_{4,0}\unicode[STIX]{x1D6E5}_{4,0}=\left[\begin{array}{@{}ccccc@{}}4 & 2 & 1 & 2 & 1\\ 2 & 3 & 2 & 1 & 0\\ 1 & 2 & 2 & 1 & 0\\ 2 & 1 & 1 & 2 & 1\\ 1 & 0 & 0 & 1 & 1\end{array}\right]\qquad ^{T}\!\unicode[STIX]{x1D6E5}_{5,0}\unicode[STIX]{x1D6E5}_{5,0}=\left[\begin{array}{@{}ccccc@{}}3 & 1 & 2 & 0 & 1\\ 1 & 3 & 2 & 1 & 0\\ 2 & 2 & 3 & 1 & 1\\ 0 & 1 & 1 & 1 & 0\\ 1 & 0 & 1 & 0 & 1\end{array}\right]\end{eqnarray}$$
Therefore the Cartan matrix of
![]() $B_{0}(k\text{GL}_{n}(q))$
cannot satisfy Theorem 3.2(b), and we conclude that all simple
$B_{0}(k\text{GL}_{n}(q))$
cannot satisfy Theorem 3.2(b), and we conclude that all simple
![]() $B_{0}(k\text{GL}_{n}(q))$
-modules lie at the end of their AR-components. Now, from the known values of the unipotent characters of
$B_{0}(k\text{GL}_{n}(q))$
-modules lie at the end of their AR-components. Now, from the known values of the unipotent characters of
![]() $\text{GL}_{n}(q)$
, we easily check using CHEVIE [Reference Geck, Hiss, Lübeck, Malle and Pfeiffer6] that the dimensions of the simple modules in
$\text{GL}_{n}(q)$
, we easily check using CHEVIE [Reference Geck, Hiss, Lübeck, Malle and Pfeiffer6] that the dimensions of the simple modules in
![]() $B_{0}(k\text{GL}_{n}(q))$
are prime to
$B_{0}(k\text{GL}_{n}(q))$
are prime to
![]() $3$
. Hence they cannot be periodic by [Reference Carlson5], as
$3$
. Hence they cannot be periodic by [Reference Carlson5], as
![]() $3^{(a-1)}$
must divide the dimension of any simple periodic module, where
$3^{(a-1)}$
must divide the dimension of any simple periodic module, where
![]() $a=$
the
$a=$
the
![]() $p$
-rank of the group, but in our case
$p$
-rank of the group, but in our case
![]() $a\geqslant 2$
. Therefore every simple
$a\geqslant 2$
. Therefore every simple
![]() $B_{0}(k\text{SL}_{n}(q))$
-module lies at the end of its AR-component by [Reference Kawata, Michler and Uno21, Lemma 1.5].
$B_{0}(k\text{SL}_{n}(q))$
-module lies at the end of its AR-component by [Reference Kawata, Michler and Uno21, Lemma 1.5].
Finally, if
![]() $G=\text{PSL}_{2}(3^{n})$
for some integer
$G=\text{PSL}_{2}(3^{n})$
for some integer
![]() $n\geqslant 2$
, then the claim follows from Theorem 3.1(c) as
$n\geqslant 2$
, then the claim follows from Theorem 3.1(c) as
![]() $G$
is a finite simple group of Lie type in defining characteristic.◻
$G$
is a finite simple group of Lie type in defining characteristic.◻
As a corollary we obtain Theorem E of the Introduction.
Acknowledgments
Both authors gratefully acknowledge financial support and the hospitality provided by the Centre Interfacultaire Bernoulli (CIB) of the École Polytechnique Fédérale de Lausanne during the writing period of this article. The second author gratefully acknowledges financial support by the funding scheme TU Nachwuchsring Individual Funding 2016 granted to the second author by the TU Kaiserslautern. The first author is grateful to the hospitality of the Faculty of Mathematics of the TU Kaiserslautern. Finally, the authors would like to thank the referees for their careful reading and their many useful comments and pieces of advice.