No CrossRef data available.
Article contents
Radial Limits of Quasiconformal Functions
Published online by Cambridge University Press: 22 January 2016
Extract
Beurling and Ahlfors [1] answered a fundamental question concerning the boundary correspondence induced by a quasiconformal mapping when they proved that the correspondence need not be given by an absolutely continuous function. They proved this by characterizing the boundary correspondences of quasiconformal mappings of the upper half-plane lm(z)>0 onto the upper half-plane lm(w)>0 under which the boundary points at infinity correspond. They proved that a necessary and sufficient condition that the strictly monotone increasing function μ(x) carrying the real axis onto itself be the boundary correspondence induced by such a quasiconformal mapping is that μ(X) should satisfy a ρ-condition
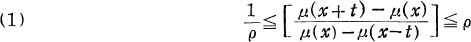
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1963

