No CrossRef data available.
Article contents
On the unramified common divisor of discriminants of integers in a normal extension
Published online by Cambridge University Press: 22 January 2016
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let F be an algebraic number field of a finite degree, and K be a normal extension over F of a finite degree n. Let 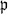 be a prime ideal of F which is unramified in K/F,
be a prime ideal of F which is unramified in K/F, 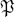 be a prime ideal of K dividing
be a prime ideal of K dividing 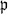 such that
such that 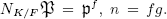 . Denote by δ(K/F) the greatest common divisor of discriminants of integers of K with respect to K/F. Then,
. Denote by δ(K/F) the greatest common divisor of discriminants of integers of K with respect to K/F. Then, 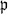 divides δ(K/F) if and only if
divides δ(K/F) if and only if 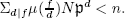
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 2000
References
[1]
Dedekind, R., Über den Zusammenhang zwuschen der Theorie der Ideale und der Theorie der höheren Kongruenzen, Abh.der König. Gesell. der Wiss. zu Göttingen, 23 (1878), 1–23, Complete works, Chelsea, 1969.Google Scholar

