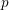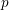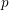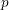Introduction
Let 
$F/k$ be a finite Galois extension of number fields with group 
$G$. Let 
$M$ be a motive defined over 
$k$ and write 
$L_{G}(M,s)$ for the complex 
$L$-function of the base change 
$M_{F}$ of 
$M$ through 
$F/k$, regarded as defined over 
$k$ and with coefficients the rational group ring 
$\mathbb{Q}[G]$.
The equivariant Tamagawa number conjecture predicts a precise connection between the leading term at 
$s=0$ of 
$L_{G}(M,s)$ and an Euler characteristic that belongs to the relative algebraic 
$K_{0}$-group of the ring extension 
$\mathbb{Z}[G]\rightarrow \mathbb{R}[G]$ and encodes the various motivic cohomology groups, realizations, comparison isomorphisms and regulators that are associated to both 
$M_{F}$ and its Kummer dual.
However, extracting fine and explicit predictions out of this technical formalism in any general setting requires detailed knowledge, for each prime 
$p$ and a suitable full Galois-stable sublattice 
$T_{p}$ of the 
$p$-adic realization of 
$M$, of the structure as 
$\mathbb{Z}_{p}[G]$-modules of (depending on the approach used) either the Bloch–Kato Selmer group 
$\text{Sel}_{F}(T_{p})$ of 
$T_{p}$ over 
$F$ or of the compactly supported 
$p$-adic étale cohomology groups 
$H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T_{p})$ for any finite set of places 
$\unicode[STIX]{x1D6F4}$ of 
$k$ that contains all archimedean places, all places which divide 
$p$ and all places at which 
$M_{F}$ has bad reduction.
In special cases there are also other strong reasons to investigate the explicit Galois structure of such cohomology groups.
For example, if 
$T_{p}=\mathbb{Z}_{p}(1)$, then 
$H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T_{p})$ identifies with the Galois group of the maximal abelian pro-
$p$ extension of 
$F$ that is unramified outside 
$\unicode[STIX]{x1D6F4}$ and aspects of the detailed Galois structures of such groups are linked to the validity, or otherwise, of Leopoldt’s conjecture. In this context such Galois structures have been much studied in the literature, both in relatively simple cases and in more involved Iwasawa-theoretic contexts (see, for example, the recent work of Khare and Wintenberger [Reference Khare and Wintenberger15]).
In another concrete direction, if 
$T_{p}$ is the 
$p$-adic Tate module of an abelian variety 
$A$ over 
$k$, then an investigation of the structure of 
$\text{Sel}_{F}(T_{p})$ as a 
$\mathbb{Z}_{p}[G]$-module can in certain circumstances be used to extract useful information concerning the changes in rank of 
$A(F^{\prime })$ as 
$F^{\prime }$ varies over intermediate fields of 
$F/k$ and to shed light on various “equivariant” refinements of the Birch and Swinnerton–Dyer conjecture for 
$A$ over 
$F$ that are studied in the literature (see, for example, the results of Macias Castillo, Wuthrich and the present author in this direction in [Reference Burns, Macias Castillo and Wuthrich7] and in the references contained therein).
Unfortunately, however, despite the interest in such investigations, understanding the explicit Galois structure of arithmetic cohomology groups in any general setting is a very difficult problem, not least because the relevant theory of integral representations is notoriously complicated (see, for example, Heller and Reiner [Reference Heller and Reiner13]).
Notwithstanding the above difficulties, in this short series of articles our aim is to show that if 
$p$ is odd, then it is possible to prove some interesting, and arithmetically useful, results concerning the structures of the 
$\mathbb{Z}_{p}[G]$-modules 
$\text{Sel}_{F}(T_{p})$, 
$H^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T_{p})$ and 
$H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T_{p})$ as 
$F$ varies in natural families of Galois extensions.
In this first note we shall establish a general “bound” on the complexity of 
$\mathbb{Z}_{p}[G]$-modules of the form 
$H^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T_{p})$ and 
$H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T_{p})$ by showing that in all cases they contain a projective direct summand with a complement the 
$p$-rank of which can be explicitly bounded (for a precise statement see Theorem 1.1).
This observation has several interesting, and (to us) quite surprising, consequences. For example, it leads to general “finiteness results” concerning indecomposable 
$\mathbb{Z}_{p}[G]$-lattices occurring as direct summands of the lattices obtained by considering 
$H^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T_{p})$ and 
$H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T_{p})$ modulo their torsion subgroups and hence, upon specialization, to concrete structure results concerning natural arithmetic modules including unit groups, higher algebraic 
$K$-groups and ray class groups (see, for example, Corollaries 3.1 and 4.1, Theorem 4.3 and the computations in Section 4.3).
In another direction, we show the result gives concrete, and very general, information about the change in rank of the Selmer groups of 
$T_{p}$ over 
$F$ and 
$k$ (see Corollary 1.2).
In subsequent articles we develop in greater detail two aspects of this general approach. First, in joint work with Kumon [Reference Burns and Kumon6], we explain how structure results for ray class groups of the sort discussed here can be used to extract concrete results and predictions from the formalism of the equivariant Tamagawa number conjecture for 
$h^{0}(\text{Spec}(F))(1)$ and, in addition, to shed new light on the validity of Leopoldt’s conjecture. Second, by using Selmer complexes defined by Nekovář in the role played here by compactly supported 
$p$-adic cohomology complexes, in [Reference Burns3] we prove analogous results about the explicit Galois structure of the Bloch–Kato Selmer groups of critical motives and so extend the results obtained by Macias Castillo, Wuthrich and the present author in [Reference Burns, Macias Castillo and Wuthrich7].
1 Statement of the main results
1.1
At the outset we fix a number field 
$k$, an algebraic closure 
$k^{c}$ of 
$k$, an odd prime 
$p$ and a finite set of places 
$\unicode[STIX]{x1D6F4}$ of 
$k$ containing the sets 
$\unicode[STIX]{x1D6F4}_{\infty }$ of all archimedean places and 
$\unicode[STIX]{x1D6F4}_{p}$ of all 
$p$-adic places and we set 
$\unicode[STIX]{x1D6F4}_{f}:=\unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$. We also write 
$k_{\unicode[STIX]{x1D6F4}}$ for the maximal extension of 
$k$ in 
$k^{c}$ that is unramified outside 
$\unicode[STIX]{x1D6F4}$ and set 
$G_{k,\unicode[STIX]{x1D6F4}}:=\text{Gal}(k_{\unicode[STIX]{x1D6F4}}/k)$.
We assume to be given a finitely generated free 
$\mathbb{Z}_{p}$-module 
$T$ of rank 
$\text{rk}(T)$ and a continuous homomorphism of the form
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}:G_{k,\unicode[STIX]{x1D6F4}}\rightarrow \text{Aut}_{\mathbb{Z}_{p}}(T). & & \displaystyle\end{eqnarray}$$ We regard 
$T$ as a left 
$\mathbb{Z}_{p}[G_{k,\unicode[STIX]{x1D6F4}}]$-module via 
$\unicode[STIX]{x1D70C}$ and write 
$T^{\ast }(1)$ for the linear Kummer dual 
$\operatorname{Hom}_{\mathbb{Z}_{p}}(T,\mathbb{Z}_{p}(1))$, regarded as a (left) 
$\mathbb{Z}_{p}[G_{k,\unicode[STIX]{x1D6F4}}]$-module via the action given by 
$(\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D703})(t)=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})^{-1}(t)))$ for all 
$\unicode[STIX]{x1D70E}$ in 
$G_{k,\unicode[STIX]{x1D6F4}}$, 
$\unicode[STIX]{x1D703}$ in 
$T^{\ast }(1)$ and 
$t$ in 
$T$.
If 
$L$ is a finite extension of 
$k$, then for any set of places 
$\unicode[STIX]{x1D6F4}^{\prime }$ of 
$k$ we write 
$\unicode[STIX]{x1D6F4}_{L}^{\prime }$ for the set of places of 
$L$ above 
$\unicode[STIX]{x1D6F4}^{\prime }$ and, if 
$\unicode[STIX]{x1D6F4}^{\prime }$ contains 
$\unicode[STIX]{x1D6F4}_{\infty }$, we write 
${\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}^{\prime }}$ for the subring of 
$L$ comprising elements that are integral at all places of 
$L$ outside 
$\unicode[STIX]{x1D6F4}_{L}^{\prime }$ and 
$\text{Cl}_{\unicode[STIX]{x1D6F4}^{\prime }}(L)$ for the ideal class group of 
${\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}^{\prime }}$.
We identify both 
$T$ and 
$T^{\ast }(1)$ with étale pro-sheaves on 
$\text{Spec}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}})$ in the usual way and for any such sheaf 
$B$ we abbreviate 
$H^{i}(\text{Spec}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}})_{\acute{\text{e}}\text{t}},B)$ and 
$H_{c}^{i}(\text{Spec}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}})_{\acute{\text{e}}\text{t}},B)$ to 
$H^{i}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}},B)$ and 
$H_{c}^{i}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}},B)$, respectively.
For a Galois extension 
$F/E$ we shall usually abbreviate the group 
$\text{Gal}(F/E)$ to 
$G_{F/E}$.
1.2
In the sequel we write 
$\unicode[STIX]{x1D707}_{p}$ for the group of 
$p$th roots of unity in 
$k^{c}$. We also write 
$k_{T}$ for the finite Galois extension of 
$k(\unicode[STIX]{x1D707}_{p})$ that corresponds to the kernel of the action of 
$G_{k(\unicode[STIX]{x1D707}_{p}),\unicode[STIX]{x1D6F4}}$ on 
$T/p$ that is induced by 
$\unicode[STIX]{x1D70C}$, and hence also to the kernel of the induced action of 
$G_{k(\unicode[STIX]{x1D707}_{p}),\unicode[STIX]{x1D6F4}}$ on 
$T^{\ast }(1)/p\cong (T/p)^{\vee }(1)$. For any extension 
$F$ of 
$k$ in 
$k^{c}$ we then write 
$F_{T}$ for the compositum 
$k_{T}F$ of 
$k_{T}$ and 
$F$.
We write 
$\mathbb{F}_{p}$ for the finite field of cardinality 
$p$ and for any finitely generated 
$\mathbb{Z}_{p}$-module 
$M$ we write 
$\text{rk}_{p}(M)$ for its “
$p$-rank” 
$\text{dim}_{\mathbb{F}_{p}}(M/p)$.
We can now state our main result.
Theorem 1.1. Let 
$F/E$ be a Galois extension of fields with 
$k\subseteq E\subseteq F\subset k^{c}$, 
$F/k$ finite and 
$F/E$ unramified outside 
$\unicode[STIX]{x1D6F4}_{E}$. Then in each degree 
$i$ there are decompositions of 
$\mathbb{Z}_{p}[G_{F/E}]$-modules
$$\begin{eqnarray}\displaystyle H^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)=P_{F/E,T}^{i}\oplus R_{F/E,T}^{i} & & \displaystyle \nonumber\end{eqnarray}$$and
$$\begin{eqnarray}H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)=P_{F/E,T,c}^{i}\oplus R_{F/E,T,c}^{i}\end{eqnarray}$$ where the modules 
$P_{F/E,T}^{i}$ and 
$P_{F/E,T,c}^{i}$ are projective and one has
$$\begin{eqnarray}\displaystyle \text{rk}_{p}(R_{F/E,T}^{i})\leqslant m_{F/E,T}^{i}\cdot \text{rk}(T)\qquad \text{and}\qquad \text{rk}_{p}(R_{F/E,T,c}^{i})\leqslant m_{F/E,T,c}^{i}\cdot \text{rk}(T) & & \displaystyle \nonumber\end{eqnarray}$$ for integers 
$m_{F/E,T}^{i}$ and 
$m_{F/E,T,c}^{i}$ depending only on 
$i$, 
$[F:E]$, 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T}))$ and 
$\#\unicode[STIX]{x1D6F4}_{f,F}$.
Explicit expressions for the integers 
$m_{F/E,T}^{i}$ and 
$m_{F/E,T,c}^{i}$ will be given in the course of the proof of Theorem 1.1 in Section 2.3.
This result is of interest as the dimensions of the 
$\mathbb{Q}_{p}$-spaces spanned by 
$H^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ and 
$H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ are in general unbounded as 
$F$ varies, whilst it is often possible to give universal bounds for both 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T}))$ and 
$\#\unicode[STIX]{x1D6F4}_{f,F}$ as 
$F$ ranges over natural families of extensions of 
$k$ of unbounded degree (see, for example, Example 3.2 and the proof of Proposition 4.2).
In addition, in Section 3 we show that for representations 
$\unicode[STIX]{x1D70C}$ of the form (1) that have pro-
$p$ image one can often weaken the explicit dependence of the bounds given in Theorem 1.1 on either 
$\unicode[STIX]{x1D70C}$ or the behavior of class groups (for details see Corollary 3.1).
In Section 3 we also deduce the following result showing that Theorem 1.1 gives concrete information about changes in the dimension 
$\text{rk}(\text{Sel}_{F}(T))$ of the 
$\mathbb{Q}_{p}$-space spanned by the Bloch–Kato Selmer group 
$\text{Sel}_{F}(T)$ of 
$T$ over finite extensions 
$F$ of 
$k$. (Note that if 
$T$ is the 
$p$-adic Tate module of an abelian variety over 
$k$ for which the classical Tate–Shafarevich group over 
$F$ is finite, then 
$\text{rk}(\text{Sel}_{F}(T))$ coincides with the dimension of the rational space spanned by the Mordell–Weil group of 
$A$ over 
$F$.)
Corollary 1.2. For each natural number 
$r$ there exists a finite Galois extension 
$k_{\unicode[STIX]{x1D6F4},r}$ of 
$k$ in 
$k_{\unicode[STIX]{x1D6F4}}$ with the following property: as 
$T$ ranges over 
$p$-adic representations of 
$G_{k,\unicode[STIX]{x1D6F4}}$ that have pro-
$p$ image and rank at most 
$r$ and 
$F/E$ over finite 
$p$-power degree Galois extensions of fields with 
$k\subseteq E\subseteq F\subset k^{c}$, 
$E/k$ finite and 
$F/E$ unramified outside 
$\unicode[STIX]{x1D6F4}_{E}$, one has
$$\begin{eqnarray}\displaystyle [F:E]\cdot \text{rk}(\text{Sel}_{E}(T))-n_{1}\leqslant \text{rk}(\text{Sel}_{F}(T))\leqslant [F:E]\cdot \text{rk}(\text{Sel}_{E}(T))+n_{2} & & \displaystyle \nonumber\end{eqnarray}$$ where 
$n_{1}$ and 
$n_{2}$ are integers that depend only on 
$[F:\mathbb{Q}]$, 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(k_{\unicode[STIX]{x1D6F4},r}F))$ and 
$\#\unicode[STIX]{x1D6F4}_{f}$ and are made explicit in Section 3.2.
Remark 1.3. The degree of 
$k_{\unicode[STIX]{x1D6F4},r}$ over 
$k$ can be large (see the proof of Corollary 3.1). As a special case, Corollary 1.2 implies the existence of constants 
$m_{1}$ and 
$m_{2}$ depending only on 
$k,\unicode[STIX]{x1D6F4}$ and 
$r$ such that for any 
$p$-adic representation 
$T$ of 
$G_{k,\unicode[STIX]{x1D6F4}}$ with pro-
$p$ image and rank at most 
$r$ and any Galois extension 
$F$ of 
$k$ of 
$p$-power degree in 
$k_{\unicode[STIX]{x1D6F4},r}$ one has
$$\begin{eqnarray}\displaystyle [F:k]\cdot \text{rk}(\text{Sel}_{k}(T))-m_{1}\leqslant \text{rk}(\text{Sel}_{F}(T))\leqslant [F:k]\cdot \text{rk}(\text{Sel}_{k}(T))+m_{2}. & & \displaystyle \nonumber\end{eqnarray}$$ This strongly restricts the structure of 
$\text{Sel}_{F}(T)$. For instance, if 
$F/k$ has degree 
$p$, then a classical result of Diederichsen [Reference Diederichsen10] implies there exist nonnegative integers 
$a_{F}(T),b_{F}(T)$ and 
$c_{F}(T)$ and an isomorphism of 
$\mathbb{Z}_{p}[G_{F/k}]$-modules of the form
$$\begin{eqnarray}\displaystyle \text{Sel}_{F}(T)_{\text{tf}}\cong \mathbb{Z}_{p}[G_{F/k}]^{a_{F}(T)}\oplus \left(\mathbb{Z}_{p}[G_{F/k}]/\biggl(\mathop{\sum }_{g\in G_{F/k}}g\biggr)\right)^{b_{F}(T)}\oplus \mathbb{Z}_{p}^{c_{F}(T)} & & \displaystyle \nonumber\end{eqnarray}$$ where 
$\text{Sel}_{F}(T)_{\text{tf}}$ denotes the quotient of 
$\text{Sel}_{F}(T)$ by its torsion subgroup, and the above inequalities now imply that
$$\begin{eqnarray}\displaystyle -m_{1}/(p-1)\leqslant b_{F}(T)-c_{F}(T)\leqslant m_{2}/(p-1). & & \displaystyle \nonumber\end{eqnarray}$$ Finally we note that Theorem 1.1 has concrete consequences concerning natural arithmetic modules (including unit groups, higher algebraic 
$K$-groups and ray class groups) and that in special cases our methods can be used to give much more explicit structural results concerning such modules. These aspects of the theory are considered in Section 4.
2 The proof of Theorem 1.1
In this section we first prove a purely algebraic result that may itself be of some independent interest. We then combine this result with some general properties of 
$p$-adic étale cohomology to prove Theorem 1.1.
For any 
$\mathbb{Z}_{p}$-module 
$X$ we write 
$X_{\text{tor}}$ for the torsion submodule of 
$X$, 
$X_{\text{tf}}$ for the quotient of 
$X$ by 
$X_{\text{tor}}$, 
$X^{\ast }$ for the linear dual 
$\operatorname{Hom}_{\mathbb{Z}_{p}}(X,\mathbb{Z}_{p})$ and 
$X^{\vee }$ for the Pontryagin dual 
$\operatorname{Hom}_{\mathbb{Z}_{p}}(X,\mathbb{Q}_{p}/\mathbb{Z}_{p})$ of continuous homomorphisms. If 
$X$ is endowed with the action of a finite group 
$G$, then we always endow both 
$X^{\ast }$ and 
$X^{\vee }$ with the natural contragredient action of 
$G$.
For any abelian group 
$X$ we write 
$X[p]$ for the subgroup of 
$X$ comprising elements annihilated by 
$p$. For any finitely generated 
$\mathbb{Z}_{p}$-module 
$X$ we set 
$\text{rk}(X):=\text{dim}_{\mathbb{Q}_{p}}(\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}X)$ and note that 
$\text{rk}_{p}(X)=\text{dim}_{\mathbb{F}_{p}}(X[p])+\text{rk}(X)$. In the sequel we also often use, without explicit comment, the fact that for any exact sequence of finitely generated 
$\mathbb{Z}_{p}$-modules 
$X_{1}\xrightarrow[{}]{\unicode[STIX]{x1D703}_{1}}X_{2}\xrightarrow[{}]{\unicode[STIX]{x1D703}_{2}}X_{3}$ one has 
$\text{rk}_{p}(\operatorname{im}(\unicode[STIX]{x1D703}_{i}))\leqslant \text{rk}_{p}(X_{2})\leqslant \text{rk}_{p}(X_{1})+\text{rk}_{p}(X_{3})$ for 
$i=1$ and 
$i=2$.
For a finite group 
$G$ we write 
$\text{tr}_{G}$ for the “trace” element 
$\sum _{g\in G}g$ of 
$\mathbb{Z}[G]$. We recall that a “
$\mathbb{Z}_{p}[G]$-lattice” is a finitely generated 
$\mathbb{Z}_{p}[G]$-module that is torsion-free.
2.1
The following result is key to our approach and may also itself be of some independent interest (see, for example, Remark 2.2).
Proposition 2.1. Let 
$G$ be a finite group of 
$p$-power order, 
$X$ a 
$\mathbb{Z}_{p}[G]$-lattice and 
$\{{x_{i}\}}_{1\leqslant i\leqslant t}$ a finite subset of 
$X$. Then the images in 
$H^{0}(G,X)/p$ of the elements 
$\{\text{tr}_{G}(x_{i})\}_{1\leqslant i\leqslant t}$ are linearly independent over 
$\mathbb{F}_{p}$ if and only if the 
$\mathbb{Z}_{p}[G]$-submodule of 
$X$ that is generated by 
$\{{x_{i}\}}_{1\leqslant i\leqslant t}$ is both a direct summand of 
$X$ and free of rank 
$t$.
Proof. Write 
${\mathcal{X}}$ for the 
$\mathbb{Z}_{p}[G]$-submodule of 
$X$ generated by 
$\{{x_{i}\}}_{1\leqslant i\leqslant t}$.
If 
${\mathcal{X}}$ is free of rank 
$t$, then 
$H^{0}(G,{\mathcal{X}})=\text{tr}_{G}({\mathcal{X}})$ is a free 
$\mathbb{Z}_{p}$-module of rank 
$t$ and is generated by the elements 
$\{\text{tr}_{G}(x_{i})\}_{1\leqslant i\leqslant t}$. The images in 
$H^{0}(G,{\mathcal{X}})/p$ of these elements are therefore linearly independent over 
$\mathbb{F}_{p}$. If, in addition, the 
$\mathbb{Z}_{p}[G]$-module 
${\mathcal{X}}$ is a direct summand of 
$X$, then the 
$\mathbb{F}_{p}$-module 
$H^{0}(G,{\mathcal{X}})/p$ is a direct summand of 
$H^{0}(G,X)/p$ and so the images in 
$H^{0}(G,X)/p$ of the given elements are also linearly independent over 
$\mathbb{F}_{p}$, as claimed.
To prove the converse implication we use the homomorphism of 
$\mathbb{Z}_{p}[G]$-modules
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}:\mathbb{Z}_{p}[G]^{t}{\twoheadrightarrow}{\mathcal{X}}\subseteq X & & \displaystyle \nonumber\end{eqnarray}$$ that sends each element 
$b_{i}$ of the standard basis 
$\{{b_{i}\}}_{1\leqslant i\leqslant t}$ of 
$\mathbb{Z}_{p}[G]^{t}$ to 
$x_{i}$.
We write 
$\overline{\unicode[STIX]{x1D713}}$ for the homomorphism 
$\mathbb{F}_{p}[G]^{t}\rightarrow X/pX$ induced by 
$\unicode[STIX]{x1D713}$ and note that if 
$\ker (\overline{\unicode[STIX]{x1D713}})$ is nontrivial, then 
$H^{0}(G,\ker (\overline{\unicode[STIX]{x1D713}}))$ is also nontrivial (as 
$G$ is a 
$p$-group). However, the group 
$H^{0}(G,\mathbb{F}_{p}[G]^{t})$ is generated by the images in 
$\mathbb{F}_{p}[G]^{t}$ of the elements 
$\text{tr}_{G}(b_{i})$ and so the nontriviality of 
$H^{0}(G,\ker (\overline{\unicode[STIX]{x1D713}}))$ would contradict the linear independence hypothesis on the elements 
$\text{tr}_{G}(x_{i})$. The map 
$\overline{\unicode[STIX]{x1D713}}$ is therefore injective and so one has 
$\ker (\unicode[STIX]{x1D713})\subseteq p\cdot \mathbb{Z}_{p}[G]^{t}$.
On the other hand, 
${\mathcal{X}}$ is a free 
$\mathbb{Z}_{p}$-module so the tautological exact sequence of 
$\mathbb{Z}_{p}$-modules 
$0\rightarrow \ker (\unicode[STIX]{x1D713})\rightarrow \mathbb{Z}_{p}[G]^{t}\rightarrow {\mathcal{X}}\rightarrow 0$ splits and one has 
$\ker (\unicode[STIX]{x1D713})=\ker (\unicode[STIX]{x1D713})\cap p\cdot \mathbb{Z}_{p}[G]^{t}=p\cdot \ker (\unicode[STIX]{x1D713})$. This shows that 
$\ker (\unicode[STIX]{x1D713})$ vanishes and hence that 
${\mathcal{X}}$ is a free 
$\mathbb{Z}_{p}[G]$-module of rank 
$t$ (as claimed).
In addition, the fact that 
${\mathcal{X}}$ is a free 
$G$-module implies both that 
$H^{0}(G,{\mathcal{X}})=\text{tr}_{G}({\mathcal{X}})$ and that the group 
$H^{1}(G,{\mathcal{X}})$ vanishes. Thus, writing 
$\unicode[STIX]{x1D704}$ for the inclusion 
${\mathcal{X}}\subseteq X$, the long exact sequence of 
$G$-cohomology associated to the tautological sequence
$$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{X}}\xrightarrow[{}]{\unicode[STIX]{x1D704}}X\rightarrow \text{cok}(\unicode[STIX]{x1D704})\rightarrow 0 & & \displaystyle\end{eqnarray}$$ gives an exact sequence of 
$\mathbb{Z}_{p}$-modules
$$\begin{eqnarray}\displaystyle 0\rightarrow \text{tr}_{G}({\mathcal{X}})\rightarrow H^{0}(G,X)\rightarrow H^{0}(G,\text{cok}(\unicode[STIX]{x1D704}))\rightarrow 0. & & \displaystyle\end{eqnarray}$$ Now, the images in 
$H^{0}(G,X)/p$ of the generating elements 
$\{\text{tr}_{G}(x_{i})\}_{1\leqslant i\leqslant t}$ of 
$\text{tr}_{G}({\mathcal{X}})$ are, by assumption, linearly independent over 
$\mathbb{F}_{p}$ and so can be extended to an 
$\mathbb{F}_{p}$-basis of 
$H^{0}(G,X)/p$. Nakayama’s lemma therefore implies that the elements 
$\{\text{tr}_{G}(x_{i})\}_{1\leqslant i\leqslant t}$ belong to a basis of the 
$\mathbb{Z}_{p}$-module 
$H^{0}(G,X)$ and, given this, the exact sequence (3) implies that the 
$\mathbb{Z}_{p}$-module 
$H^{0}(G,\text{cok}(\unicode[STIX]{x1D704}))$ is free. This in turn implies that the module 
$H^{0}(G,\text{cok}(\unicode[STIX]{x1D704}))_{\text{tor}}=H^{0}(G,\text{cok}(\unicode[STIX]{x1D704})_{\text{tor}})$ vanishes, and hence, since 
$G$ is a 
$p$-group, that the module 
$\text{cok}(\unicode[STIX]{x1D704})_{\text{tor}}$ itself vanishes.
Then, as 
$\text{cok}(\unicode[STIX]{x1D704})$ is free over 
$\mathbb{Z}_{p}$, the exact sequence (2) induces, upon taking linear duals, an exact sequence of 
$\mathbb{Z}_{p}[G]$-modules
$$\begin{eqnarray}\displaystyle 0\rightarrow \text{cok}(\unicode[STIX]{x1D704})^{\ast }\rightarrow X^{\ast }\xrightarrow[{}]{\unicode[STIX]{x1D704}^{\ast }}{\mathcal{X}}^{\ast }\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$ Since the 
$\mathbb{Z}_{p}[G]$-module 
$\mathbb{Z}_{p}[G]^{\ast }$ is free of rank one (by, for example, [Reference Curtis and Reiner8, Theorem (10.29)]), the 
$\mathbb{Z}_{p}[G]$-module 
${\mathcal{X}}^{\ast }$ is free of rank 
$t$ and so this sequence splits. Thus, upon taking linear duals, one deduces that (2) also splits as a sequence of 
$\mathbb{Z}_{p}[G]$-modules, as required to complete the proof.◻
Remark 2.2. The result of Proposition 2.1 leads immediately to the following observation regarding indecomposable lattices: if 
$G$ is any finite 
$p$-group and 
$I$ any indecomposable 
$\mathbb{Z}_{p}[G]$-lattice, then either 
$\text{tr}_{G}(I)$ is contained in 
$p\cdot H^{0}(G,I)$ or 
$I$ is isomorphic to 
$\mathbb{Z}_{p}[G]$.
2.2
In this section we fix an odd prime 
$p$ and data 
$F/E,\unicode[STIX]{x1D6F4}$ and 
$T$ as in Theorem 1.1 and set 
$G:=G_{F/E}$. For any noetherian ring 
$R$ we write 
$D(R)$ for the derived category of left 
$R$-modules and 
$D^{\text{p}}(R)$ for the full triangulated subcategory of 
$D(R)$ comprising perfect complexes.
In the following result we record some relevant (and essentially well-known) properties of the compactly supported étale cohomology complexes 
$R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ that arise in the context of Theorem 1.1. We recall that these complexes are defined so as to lie in natural exact triangles in 
$D(\mathbb{Z}_{p}[G])$ of the form
$$\begin{eqnarray}\displaystyle \qquad R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)\rightarrow R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)\rightarrow \bigoplus _{w\in \unicode[STIX]{x1D6F4}_{F}}R\unicode[STIX]{x1D6E4}(F_{w},T)\rightarrow R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)[1], & & \displaystyle\end{eqnarray}$$with the second arrow denoting the natural diagonal localization map.
In the sequel we also set 
$B_{F}(T):=\bigoplus _{w\in \unicode[STIX]{x1D6F4}_{\infty ,F}}H^{0}(F_{w},T)$.
Proposition 2.3. For data 
$F/E,\unicode[STIX]{x1D6F4},T$ and 
$G$ as above the following claims are valid.
(i) Let
$J$ be a normal subgroup of $G$. Then there are natural isomorphisms in $D(\mathbb{Z}_{p}[G_{F^{J}/E}])$$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}\mathbb{Z}_{p}[G_{F^{J}/E}]\otimes _{\mathbb{Z}_{p}[G]}^{\mathbb{L}}R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)\cong R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F^{J},\unicode[STIX]{x1D6F4}},T),\quad \\ \mathbb{Z}_{p}[G_{F^{J}/E}]\otimes _{\mathbb{Z}_{p}[G]}^{\mathbb{L}}R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)\cong R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F^{J},\unicode[STIX]{x1D6F4}},T).\quad \end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$(ii) The complexes
$R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ and $R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ are respectively acyclic outside degrees zero, one and two and degrees one, two and three. In addition, there is an isomorphism of $\mathbb{Z}_{p}[G]$-modules (5)and for both$$\begin{eqnarray}\displaystyle H_{c}^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)\cong B_{F}(T)\oplus H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast } & & \displaystyle\end{eqnarray}$$$i=2$ and $i=3$ a canonical short exact sequence of $\mathbb{Z}_{p}[G]$-modules (6)$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle (H^{4-i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))_{\text{tor}})^{\vee }\rightarrow H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)\nonumber\\ \displaystyle & \rightarrow & \displaystyle H^{3-i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast }\rightarrow 0.\end{eqnarray}$$(iii)
$R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ and $R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ belong to $D^{\text{p}}(\mathbb{Z}_{p}[G])$.(iv) The Euler characteristic of
$R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ in $K_{0}(\mathbb{Z}_{p}[G])$ vanishes.
Proof. The first isomorphism in claim (i) is the standard “projection formula” isomorphism in étale cohomology. The second isomorphism then results by combining this with the analogous isomorphisms for the complexes 
$R\unicode[STIX]{x1D6E4}(F_{w},T)$ and the definition of compactly supported cohomology via the triangles (4) for 
$F$ and 
$F^{J}$.
Next we note that, since 
$p$ is odd, the complex 
$R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ is well known to be acyclic outside degrees zero, one and two. In addition, setting 
$C:=R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))$, the Artin–Verdier duality theorem implies there is a canonical exact triangle in 
$D(\mathbb{Z}_{p}[G])$
$$\begin{eqnarray}\displaystyle B_{F}(T)[-1]\rightarrow R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)\rightarrow R\operatorname{Hom}_{\mathbb{Z}_{p}}(C,\mathbb{Z}_{p}[-3])\rightarrow B_{F}(T)[0] & & \displaystyle\end{eqnarray}$$(see, for example, [Reference Burns and Flach5, Lemma 12b]). By using the universal coefficient spectral sequence
$$\begin{eqnarray}\displaystyle E_{2}^{p,q}=\text{Ext}_{\mathbb{Z}_{p}}^{p}(H^{3-q}(C),\mathbb{Z}_{p})\Longrightarrow H^{p+q}(R\operatorname{Hom}_{\mathbb{Z}_{p}}(C,\mathbb{Z}_{p}[-3])) & & \displaystyle \nonumber\end{eqnarray}$$ (cf. [Reference Verdier19, III.4.6.10]) one can also compute the cohomology groups of the third term in the above triangle in terms of those of 
$C$.
In this way one finds the long exact sequence of cohomology of (7) implies 
$R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ is acyclic outside degrees one, two and three and gives rise both to the exact sequences (6) and also to a short exact sequence 
$0\rightarrow B_{F}(T)\rightarrow H_{c}^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)\rightarrow H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast }\rightarrow 0$. In addition, since 
$B_{F}(T)$ is a projective 
$\mathbb{Z}_{p}[G]$-module (by Lemma 2.4(i) below) and the module 
$H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast }$ is torsion-free, the same argument as used at the end of the proof of Proposition 2.1 shows this sequence of 
$\mathbb{Z}_{p}[G]$-modules splits to give an isomorphism of the form (5), as required to complete the proof of claim (ii).
Finally, we note that claims (iii) and (iv) are special cases of a result of Flach [Reference Flach11, Theorem 5.1] and of Flach and the present author [Reference Burns and Flach5, Lemma 7], respectively. ◻
In the sequel we will also find the following observations to be useful.
Lemma 2.4. For data 
$F/E,T$ and 
$G$ as in Proposition 2.3 the following claims are valid.
(i)
$B_{F}(T)$ is a projective $\mathbb{Z}_{p}[G]$-module.(ii) If
$J$ is any subgroup of $G$ of odd order, then $\text{rk}(B_{F}(T))$ is equal to $\#J\cdot \text{rk}(B_{F^{J}}(T))$.
Proof. For each place 
$v$ in 
$\unicode[STIX]{x1D6F4}_{\infty ,E}$ we choose a corresponding embedding 
$\unicode[STIX]{x1D70E}_{v}:E\rightarrow E_{v}$ and write 
$G_{v}$ for the decomposition subgroup in 
$G$ of a fixed place of 
$F$ above 
$v$. Then there is a natural isomorphism of 
$\mathbb{Z}_{p}[G]$-modules
$$\begin{eqnarray}\displaystyle B_{F}(T)\cong \bigoplus _{v\in \unicode[STIX]{x1D6F4}_{\infty ,E}}H^{0}\biggl(G_{v},T\otimes _{\mathbb{Z}_{p}}\mathop{\prod }_{\unicode[STIX]{x1D6F4}_{v}}\mathbb{Z}_{p}\biggr) & & \displaystyle \nonumber\end{eqnarray}$$ where 
$\unicode[STIX]{x1D6F4}_{v}$ denotes the set of embeddings 
$F\rightarrow (E_{v})^{c}$ that extend 
$\unicode[STIX]{x1D70E}_{v}$ and on the tensor product 
$G_{v}$ acts diagonally (via postcomposition with elements of 
$\unicode[STIX]{x1D6F4}_{v}$) and 
$G$ acts only on the second factor (via precomposition with elements of 
$\unicode[STIX]{x1D6F4}_{v}$).
This isomorphism immediately implies claim (i) since each 
$\mathbb{Z}_{p}[G]$-module 
$T\otimes _{\mathbb{Z}_{p}}\prod _{\unicode[STIX]{x1D6F4}_{v}}\mathbb{Z}_{p}$ is free and the order of each subgroup 
$G_{v}$ is prime to 
$p$.
If 
$\#J$ is odd, then each place 
$v$ in 
$\unicode[STIX]{x1D6F4}_{\infty ,E}$ is totally split in 
$F/F^{J}$. This implies that there are isomorphisms of 
$\mathbb{Z}_{p}$-modules
$$\begin{eqnarray}\displaystyle B_{F}(T) & = & \displaystyle \mathop{\bigoplus }_{w\in \unicode[STIX]{x1D6F4}_{\infty ,F}}H^{0}(G_{w},T)\nonumber\\ \displaystyle & \cong & \displaystyle \mathbb{Z}_{p}[J]\otimes _{\mathbb{Z}_{p}}\biggl(\mathop{\bigoplus }_{s\in \unicode[STIX]{x1D6F4}_{\infty ,F^{J}}}H^{0}(G_{s},T)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathbb{Z}_{p}[J]\otimes _{\mathbb{Z}_{p}}B_{F^{J}}(T).\nonumber\end{eqnarray}$$Claim (ii) follows immediately from this composite isomorphism. ◻
2.3
Turning now to the proof of Theorem 1.1 we proceed by a number of reductions.
In the sequel we often use, without explicit comment, the fact that the numbers 
$\text{rk}(T)$ and 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T}))$ are both unchanged if one replaces 
$T$ by 
$T^{\ast }(1)$.
Lemma 2.5. It is enough to prove the result of Theorem 1.1 as it applies to 
$H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$.
Proof. At the outset we note 
$H^{0}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ is a submodule of 
$T$ and hence that in this case the claim of Theorem 1.1 is obviously true with 
$P_{F/E,T}^{0}=0$ and 
$m_{F/E,T}^{0}=1$.
Next, the long exact cohomology sequence of the sequence
$$\begin{eqnarray}\displaystyle 0\rightarrow T\xrightarrow[{}]{p}T\rightarrow T/p\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ induces both a surjective homomorphism 
$H^{0}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T/p)\rightarrow H^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)[p]$ and an isomorphism 
$H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)/p\cong H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T/p)$, and hence implies 
$\text{rk}_{p}(H^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)[p])\leqslant \text{rk}(T)$ and 
$\text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T))=\text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T/p))$, respectively.
The inequality 
$\text{rk}_{p}(H^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)[p])\leqslant \text{rk}(T)$ combines with the exact sequences (6) (with 
$T$ replaced by 
$T^{\ast }(1)$) to give two consequences.
First, it implies a decomposition of the required sort for 
$H_{c}^{3}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ with 
$P_{F/E,T,c}^{3}=0$ and 
$m_{F/E,T,c}^{3}=2$.
Second, since (6) implies 
$H^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)_{\text{tf}}$ is naturally isomorphic to 
$H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast }$, it shows that a decomposition of the claimed sort for 
$H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))$ implies a corresponding decomposition of 
$H^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ with 
$m_{F/E,T}^{1}=m_{F/E,T,c}^{2}+1$.
We now note that, since the complexes 
$R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},T)$ and 
$R\unicode[STIX]{x1D6E4}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ are acyclic in degrees greater than two the first descent isomorphism in Proposition 2.3(i) induces an identification 
$H_{0}(G_{F_{T}/F},H^{2}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},T))\cong H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ and hence implies that
$$\begin{eqnarray}\displaystyle \text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)) & {\leqslant} & \displaystyle \text{rk}_{p}(H^{2}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},T))\nonumber\\ \displaystyle & = & \displaystyle \text{rk}_{p}(H^{2}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},T/p))\nonumber\\ \displaystyle & = & \displaystyle \text{rk}(T)\cdot \text{rk}_{p}(H^{2}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},\unicode[STIX]{x1D707}_{p}))\nonumber\\ \displaystyle & = & \displaystyle \text{rk}(T)\cdot (\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T}))+\#\unicode[STIX]{x1D6F4}_{f,F_{T}}-1).\end{eqnarray}$$ Here the second equality follows from the fact that over 
$F_{T}$ the module 
$T/p$ is isomorphic to a direct sum of 
$\text{rk}(T)$ copies of 
$\unicode[STIX]{x1D707}_{p}$ and the last follows by combining the canonical short exact sequence
$$\begin{eqnarray}\displaystyle 0\rightarrow H^{1}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},\mathbb{G}_{m})/p\rightarrow H^{2}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},\unicode[STIX]{x1D707}_{p})\rightarrow H^{2}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},\mathbb{G}_{m})[p]\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ with the fact 
$H^{1}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},\mathbb{G}_{m})=\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T})$ and an explicit computation of 
$H^{2}({\mathcal{O}}_{F_{T},\unicode[STIX]{x1D6F4}},\mathbb{G}_{m})$ using class field theory (as, for example, in [Reference Milne16, Chapter III, Example 2.22, Case (f)]).
This immediately gives a decomposition for 
$H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ of the required sort with 
$P_{F/E,T}^{2}=0$ and 
$m_{F/E,T}^{2}=\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T}))+[F_{T}:F]\cdot \#\unicode[STIX]{x1D6F4}_{f,F}-1$.
We observe finally this decomposition (with 
$T$ replaced by 
$T^{\ast }(1)$) combines with the isomorphism (5) to give a corresponding decomposition of 
$H_{c}^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ with 
$m_{F/E,T,c}^{1}=m_{F/E,T}^{2}$.◻
In the sequel, for any finite group 
$\unicode[STIX]{x1D6E4}$, any 
$\unicode[STIX]{x1D6E4}$-module 
$Y$ and any integer 
$i$ we write 
${\hat{H}}^{i}(\unicode[STIX]{x1D6E4},Y)$ for the Tate cohomology group of 
$Y$ in degree 
$i$, as discussed for example in [Reference Atiyah, Wall, Cassels and Fröhlich1, Section 6].
Since Lemma 2.5 allows us to focus on the module 
$H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ we now set
$$\begin{eqnarray}\displaystyle X:=H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T). & & \displaystyle \nonumber\end{eqnarray}$$ We also abbreviate 
$G_{F/E}$ to 
$G$.
Lemma 2.6. Theorem 1.1 is valid if and only if 
$\text{rk}_{p}({\hat{H}}^{0}(G,X_{\text{tf}}))$ is bounded by an explicit multiple of 
$\text{rk}(T)$ depending only on 
$\#G$, 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T}))$ and 
$\#\unicode[STIX]{x1D6F4}_{f,F}$.
Proof. Necessity of the given condition is clear. To prove sufficiency we note first that the exact sequence (6) implies
$$\begin{eqnarray}\displaystyle \text{rk}_{p}(X_{\text{tor}})=\text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))_{\text{tor}})\leqslant \text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))). & & \displaystyle\end{eqnarray}$$ This combines with the bound (8) (with 
$T$ replaced by 
$T^{\ast }(1)$) to show that 
$X$ has a decomposition of the form stated in Theorem 1.1 if and only if the lattice 
$X_{\text{tf}}$ has the same sort of decomposition.
To analyse 
$X_{\text{tf}}$ we fix a Sylow 
$p$-subgroup 
$P$ of 
$G$ and note the natural restriction map 
${\hat{H}}^{0}(G,X_{\text{tf}})\rightarrow {\hat{H}}^{0}(P,X_{\text{tf}})$ is bijective (as a consequence of [Reference Atiyah, Wall, Cassels and Fröhlich1, Proposition 8]).
We set
$$\begin{eqnarray}\displaystyle r:=\text{rk}(H^{0}(P,X_{\text{tf}}))\qquad \text{and}\qquad r_{p}:=\text{rk}_{p}({\hat{H}}^{0}(P,X_{\text{tf}}))=\text{rk}_{p}({\hat{H}}^{0}(G,X_{\text{tf}})), & & \displaystyle \nonumber\end{eqnarray}$$note that the integer
$$\begin{eqnarray}\displaystyle d:=r-r_{p}=\text{rk}_{p}(H^{0}(P,X_{\text{tf}})/p)-\text{rk}_{p}(H^{0}(P,X_{\text{tf}})/(p,\text{tr}_{P}(X_{\text{tf}}))) & & \displaystyle \nonumber\end{eqnarray}$$ is nonnegative and choose a set of elements 
$\{{x_{i}\}}_{1\leqslant i\leqslant d}$ of 
$X$ such that the images in 
$H^{0}(P,X_{\text{tf}})/p$ of the elements 
$\text{tr}_{P}(x_{i})$ are linearly independent over 
$\mathbb{F}_{p}$.
By applying Proposition 2.1 to this data we deduce that the 
$\mathbb{Z}_{p}[P]$-submodule 
$X^{\prime }$ of 
$X$ generated by 
$\{{x_{i}\}}_{1\leqslant i\leqslant d}$ is both free of rank 
$d$ and a direct summand of 
$X$. Fixing a complement 
$X^{\prime \prime }$ to the direct summand 
$X^{\prime }$ in 
$X$ one has
$$\begin{eqnarray}\displaystyle \text{rk}(X^{\prime \prime }) & = & \displaystyle \text{rk}(X)-\text{rk}(X^{\prime })=\text{rk}(X)-\#P\cdot d\nonumber\\ \displaystyle & = & \displaystyle (\text{rk}(X)-\#P\cdot \text{rk}(H^{0}(P,X)))+\#P\cdot r_{p}.\end{eqnarray}$$ Now, if 
$J$ denotes either 
$P$ or the identity subgroup of 
$G$, then one has
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{rk}(H^{0}(J,X))\nonumber\\ \displaystyle & & \displaystyle \quad =\text{rk}(H_{c}^{2}({\mathcal{O}}_{F^{J},\unicode[STIX]{x1D6F4}},T))\nonumber\\ \displaystyle & & \displaystyle \quad =\text{rk}(H_{c}^{1}({\mathcal{O}}_{F^{J},\unicode[STIX]{x1D6F4}},T))+\text{rk}(H_{c}^{3}({\mathcal{O}}_{F^{J},\unicode[STIX]{x1D6F4}},T))\nonumber\\ \displaystyle & & \displaystyle \quad =\text{rk}(B_{F^{J}}(T))+\text{rk}(H^{2}({\mathcal{O}}_{F^{J},\unicode[STIX]{x1D6F4}},T^{\ast }(1)))+\text{rk}(H^{0}({\mathcal{O}}_{F^{J},\unicode[STIX]{x1D6F4}},T^{\ast }(1))).\nonumber\end{eqnarray}$$(The second equality here is a consequence of Proposition 2.3(iv) and the third a consequence of the descriptions given in Proposition 2.3(ii)).
Taken in conjunction with Lemma 2.4(ii), the last displayed equality implies that
$$\begin{eqnarray}\displaystyle \text{rk}(X)-\#P\cdot \text{rk}(H^{0}(P,X)) & {\leqslant} & \displaystyle \text{rk}(X)-\#P\cdot \text{rk}(B_{F^{P}}(T))\nonumber\\ \displaystyle & = & \displaystyle \text{rk}(X)-\text{rk}(B_{F}(T))\nonumber\\ \displaystyle & = & \displaystyle \text{rk}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1)))+\text{rk}(H^{0}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1)))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \text{rk}(T)(m_{F/E,T}^{2}+1),\nonumber\end{eqnarray}$$ where 
$m_{F/E,T}^{2}$ is the explicit integer defined in the proof of Lemma 2.5.
This fact combines with (10) to imply there is an isomorphism of 
$\mathbb{Z}_{p}[G]$-modules
$$\begin{eqnarray}\displaystyle \mathbb{Z}_{p}[G]\otimes _{\mathbb{Z}_{p}[P]}X\cong X_{1}\oplus X_{2} & & \displaystyle\end{eqnarray}$$ where 
$X_{1}:=\mathbb{Z}_{p}[G]\otimes _{\mathbb{Z}_{p}[P]}X^{\prime }$ is free and 
$X_{2}:=\mathbb{Z}_{p}[G]\otimes _{\mathbb{Z}_{p}[P]}X^{\prime \prime }$ satisfies
$$\begin{eqnarray}\displaystyle \qquad \text{rk}(X_{2})=[G:P]\cdot \text{rk}(X^{\prime \prime })\leqslant [G:P]\cdot \text{rk}(T)\cdot (m_{F/E,T}^{2}+1)+\#G\cdot r_{p}. & & \displaystyle\end{eqnarray}$$ We next claim that 
$X_{\text{tf}}$ is a direct summand of the 
$\mathbb{Z}_{p}[G]$-module 
$\mathbb{Z}_{p}[G]\otimes _{\mathbb{Z}_{p}[P]}X_{\text{tf}}$. To show this write 
$t$ for the index of 
$P$ in 
$G$ and choose a set of coset representatives 
$\{{c_{i}\}}_{1\leqslant i\leqslant t}$ for 
$P$ in 
$G$. Then 
$t$ is prime to 
$p$ and the homomorphism of 
$\mathbb{Z}_{p}[G]$-modules 
$X_{\text{tf}}\rightarrow \mathbb{Z}_{p}[G]\otimes _{\mathbb{Z}_{p}[P]}X_{\text{tf}}$ that sends each 
$x$ to 
$t^{-1}\sum _{i=1}^{i=t}c_{i}^{-1}\otimes c_{i}(x)$ is a section to the natural surjective map 
$\mathbb{Z}_{p}[G]\otimes _{\mathbb{Z}_{p}[P]}X_{\text{tf}}\rightarrow X_{\text{tf}}$, as required.
In particular, if one decomposes 
$X_{\text{tf}}$ as a direct sum of 
$\mathbb{Z}_{p}[G]$-modules 
$\unicode[STIX]{x1D6F1}\oplus \unicode[STIX]{x1D6F1}^{\prime }$ where 
$\unicode[STIX]{x1D6F1}$ is projective and 
$\unicode[STIX]{x1D6F1}^{\prime }$ is a direct sum of nonprojective indecomposable modules, then the isomorphism (11) and upper bound (12) combine with the Krull–Schmidt theorem to imply that 
$\unicode[STIX]{x1D6F1}^{\prime }$ is isomorphic to a direct summand of 
$X_{2}$ and hence that
$$\begin{eqnarray}\displaystyle \text{rk}_{p}(X_{2})\leqslant [G:P]\cdot \text{rk}(T)\cdot (m_{F/E,T}^{2}+1)+\#G\cdot r_{p}. & & \displaystyle \nonumber\end{eqnarray}$$The claimed result now follows immediately from Lemma 2.5. ◻
In view of Lemma 2.6 the proof of Theorem 1.1 is completed by the following result.
Lemma 2.7. One has
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{rk}_{p}({\hat{H}}^{0}(G,X_{\text{tf}}))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \text{rk}(T)\cdot \#G\cdot (2+(1+\#G)(\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T}))+\#\unicode[STIX]{x1D6F4}_{f,F_{T}}-1)).\nonumber\end{eqnarray}$$Proof. Since Proposition 2.3 implies 
$R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ is perfect over 
$\mathbb{Z}_{p}[G]$ and acyclic outside degrees one, two and three a standard argument of homological algebra (as, for example, in [Reference Deligne9, Rapport, Lemma 4.7]) shows that this complex is isomorphic in 
$D(\mathbb{Z}_{p}[G])$ to a complex of finitely generated 
$\mathbb{Z}_{p}[G]$-modules of the form
$$\begin{eqnarray}\displaystyle Q^{1}\xrightarrow[{}]{d^{1}}Q^{2}\xrightarrow[{}]{d^{2}}Q^{3} & & \displaystyle \nonumber\end{eqnarray}$$ where each module 
$Q^{i}$ occurs in degree 
$i$, the modules 
$Q^{2}$ and 
$Q^{3}$ are free and 
$Q^{1}$ is cohomologically trivial for 
$G$. This representative of 
$R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ in turn gives rise to tautological short exact sequences of 
$\mathbb{Z}_{p}[G]$-modules
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}ll@{}}0\rightarrow X^{1}\rightarrow Q^{1}\rightarrow \operatorname{im}(d^{1})\rightarrow 0,\quad & 0\rightarrow \operatorname{im}(d^{1})\rightarrow \ker (d^{2})\rightarrow X^{2}\rightarrow 0,\\ 0\rightarrow \ker (d^{2})\rightarrow Q^{2}\rightarrow \operatorname{im}(d^{2})\rightarrow 0,\quad & 0\rightarrow \operatorname{im}(d^{2})\rightarrow Q^{3}\rightarrow X^{3}\rightarrow 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$ where we set 
$X^{i}:=H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)$ in each degree 
$i$ (so that 
$X^{2}=X$).
Since the modules 
$Q^{1},Q^{2}$ and 
$Q^{3}$ are cohomologically trivial over 
$G$, the long exact cohomology sequences of these sequences combine to give an exact sequence
$$\begin{eqnarray}\displaystyle {\hat{H}}^{-2}(G,X^{3})\rightarrow {\hat{H}}^{0}(G,X)\rightarrow {\hat{H}}^{2}(G,H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast }). & & \displaystyle \nonumber\end{eqnarray}$$ Here we also use the fact that Lemma 2.4(i) combines with the isomorphism (5) to imply the groups 
${\hat{H}}^{2}(G,X^{1})$ and 
${\hat{H}}^{2}(G,H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast })$ are naturally isomorphic.
In addition, the tautological exact sequence 
$0\rightarrow X_{\text{tor}}\rightarrow X\rightarrow X_{\text{tf}}\rightarrow 0$ also gives rise to an exact sequence 
${\hat{H}}^{0}(G,X)\rightarrow {\hat{H}}^{0}(G,X_{\text{tf}})\rightarrow H^{1}(G,X_{\text{tor}})$ and this combines with the last displayed exact sequence to imply that the 
$p$-rank 
$\text{rk}_{p}({\hat{H}}^{0}(G,X_{\text{tf}}))$ is at most
$$\begin{eqnarray}\displaystyle & & \displaystyle \!\!\text{rk}_{p}({\hat{H}}^{0}(G,X))+\text{rk}_{p}(H^{1}(G,X_{\text{tor}}))\nonumber\\ \displaystyle & & \displaystyle \!\!\quad \leqslant \text{rk}_{p}({\hat{H}}^{-2}(G,X^{3}))+\text{rk}_{p}({\hat{H}}^{2}(G,H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast }))+\text{rk}_{p}(H^{1}(G,X_{\text{tor}}))\nonumber\\ \displaystyle & & \displaystyle \!\!\quad \leqslant \#G\cdot \text{rk}_{p}(X^{3})+(\#G)^{2}\cdot \text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast })+\#G\cdot \text{rk}_{p}(X_{\text{tor}})\nonumber\\ \displaystyle & & \displaystyle \!\!\quad \leqslant \#G\cdot [\text{rk}_{p}(X^{3})+\#G\cdot \text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast })+\text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1)))]\nonumber\\ \displaystyle & & \displaystyle \!\!\quad \leqslant \#G\cdot \text{rk}(T)\cdot [2+(\#G+1)(\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{T}))+\#\unicode[STIX]{x1D6F4}_{f,F_{T}}-1)],\nonumber\end{eqnarray}$$ where the second inequality is obtained by three applications of Lemma 2.8, the third follows from (9) and the last is a consequence of the bound 
$\text{rk}_{p}(X^{3})\leqslant 2\cdot \text{rk}(T)$ obtained in the course of proving Lemma 2.5 and the bound for 
$\text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1))^{\ast })\leqslant \text{rk}_{p}(H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T^{\ast }(1)))$ given by (8). This proves the claimed result.◻
Lemma 2.8. Let 
${\mathcal{G}}$ be a finite group and 
$X$ a finitely generated 
$\mathbb{Z}_{p}[{\mathcal{G}}]$-module. Then for each integer 
$i$ one has
$$\begin{eqnarray}\displaystyle \text{rk}_{p}({\hat{H}}^{i}({\mathcal{G}},X))\leqslant (\#{\mathcal{G}})^{n_{i}}\cdot \text{rk}_{p}(X) & & \displaystyle \nonumber\end{eqnarray}$$ with 
$n_{i}$ equal to 
$i$ if 
$i\geqslant 0$ and to 
$-(i+1)$ if 
$i<0$.
Proof. The tensor product 
$X\otimes _{\mathbb{Z}_{p}}\mathbb{Z}_{p}[{\mathcal{G}}]$ is endowed with a natural diagonal action of 
${\mathcal{G}}$ and lies in two natural short exact sequences of 
$\mathbb{Z}_{p}[{\mathcal{G}}]$-modules
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}0\rightarrow X\xrightarrow[{}]{\unicode[STIX]{x1D704}_{X}}X\otimes _{\mathbb{Z}_{p}}\mathbb{Z}_{p}[{\mathcal{G}}]\rightarrow \text{cok}(\unicode[STIX]{x1D704}_{X})\rightarrow 0\quad \\ 0\rightarrow \ker (\unicode[STIX]{x1D70B}_{X})\rightarrow X\otimes _{\mathbb{Z}_{p}}\mathbb{Z}_{p}[{\mathcal{G}}]\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{X}}X\rightarrow 0.\quad \end{array}\right.\end{eqnarray}$$ These sequences imply 
$\text{rk}_{p}(\text{cok}(\unicode[STIX]{x1D704}_{X}))$ and 
$\text{rk}_{p}(\text{ker}(\unicode[STIX]{x1D70B}_{X}))$ are both at most 
$\text{rk}_{p}(X\otimes _{\mathbb{Z}_{p}}\mathbb{Z}_{p}[{\mathcal{G}}])=\#{\mathcal{G}}\cdot \text{rk}_{p}(X)$. In addition, since 
$X\otimes _{\mathbb{Z}_{p}}\mathbb{Z}_{p}[{\mathcal{G}}]$ is a cohomologically trivial 
${\mathcal{G}}$-module, the long exact cohomology sequences associated to these sequences induce isomorphisms
$$\begin{eqnarray}\displaystyle \quad {\hat{H}}^{i}({\mathcal{G}},X)\cong {\hat{H}}^{i-1}({\mathcal{G}},\text{cok}(\unicode[STIX]{x1D704}_{X}))\!\!\qquad \text{and}\qquad \!\!{\hat{H}}^{i}({\mathcal{G}},X)\cong {\hat{H}}^{i+1}({\mathcal{G}},\ker (\unicode[STIX]{x1D70B}_{X})).\hspace{-18.0pt} & & \displaystyle\end{eqnarray}$$ In particular, if 
$i\geqslant 0$, respectively 
$i<0$, then after repeatedly applying isomorphisms of the first, respectively second, kind in (13) one finds that
$$\begin{eqnarray}\displaystyle \text{rk}_{p}({\hat{H}}^{i}({\mathcal{G}},X))=\left\{\begin{array}{@{}ll@{}}\text{rk}_{p}({\hat{H}}^{0}({\mathcal{G}},X_{i}))\quad & \text{if}~i\geqslant 0,\\ \text{rk}_{p}({\hat{H}}^{-1}({\mathcal{G}},X_{i}))\quad & \text{if}~i<0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$ where in each case 
$X_{i}$ is a 
$\mathbb{Z}_{p}[{\mathcal{G}}]$-module with 
$\text{rk}_{p}(X_{i})\leqslant (\#{\mathcal{G}})^{n_{i}}\cdot \text{rk}_{p}(X)$.
The claimed result thus follows from the last displayed equality since both of the groups 
${\hat{H}}^{0}({\mathcal{G}},X_{i})$ and 
${\hat{H}}^{-1}({\mathcal{G}},X_{i})$ are, by definition, subquotients of 
$X_{i}$ and hence of 
$p$-rank at most 
$\text{rk}_{p}(X_{i})$.◻
3 Representations with pro-$p$ image
In this section we discuss applications of Theorem 1.1 in the setting of representations with pro-
$p$ image.
3.1
We start by deducing a result which shows that, in certain natural cases, one can weaken the explicit dependence of the bounds given in Theorem 1.1 on either the given 
$p$-adic representation or the behavior of class groups.
In the sequel we write 
$k_{\unicode[STIX]{x1D6F4}}^{p}$ for the maximal pro-
$p$ extension of 
$k$ in 
$k_{\unicode[STIX]{x1D6F4}}$ and 
$k_{\unicode[STIX]{x1D6F4}}^{p,\text{ab}}$ for the maximal abelian extension of 
$k$ in 
$k_{\unicode[STIX]{x1D6F4}}^{p}$.
Corollary 3.1. Fix an abstract finite group 
${\mathcal{G}}$, a finite set 
$\unicode[STIX]{x1D6F4}$ of places of 
$k$ containing 
$\unicode[STIX]{x1D6F4}_{\infty }\cup \unicode[STIX]{x1D6F4}_{p}$ and natural numbers 
$r$ and 
$b$.
Then there exists a finite Galois extension 
$k_{\unicode[STIX]{x1D6F4},r}$ of 
$k$ in 
$k_{\unicode[STIX]{x1D6F4}}$ with the following property: as 
$T$ ranges over all 
$p$-adic representations of 
$G_{k,\unicode[STIX]{x1D6F4}}$ that have pro-
$p$ image and rank at most 
$r$ and 
$F/E$ over all 
${\mathcal{G}}$-extensions of number fields that contain 
$k$, are unramified outside 
$\unicode[STIX]{x1D6F4}_{E}$ and such that 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(k_{\unicode[STIX]{x1D6F4},r}F))+\#\unicode[STIX]{x1D6F4}_{f,F}\leqslant b$, there are, up to projective direct summands, only finitely many isomorphism classes of 
$\mathbb{Z}_{p}[{\mathcal{G}}]$-modules that can arise from the modules 
$H^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)_{\text{tf}}$ and 
$H_{c}^{i}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)_{\text{tf}}$ for any choice of degree 
$i$.
Proof. If 
$\unicode[STIX]{x1D70C}$ is a representation 
$G_{k,\unicode[STIX]{x1D6F4}}\rightarrow \text{Aut}_{\mathbb{Z}_{p}}(T)$ with pro-
$p$ image and rank at most 
$r$, then the kernel of the induced modular representation 
$G_{k,\unicode[STIX]{x1D6F4}}\rightarrow \text{Aut}_{\mathbb{Z}_{p}}(T/p)$ can be computed as the kernel of a homomorphism 
$G_{k,\unicode[STIX]{x1D6F4}}\rightarrow \text{GL}_{r}(\mathbb{F}_{p})$ with pro-
$p$ image and so has index dividing the maximal power 
$p^{i_{r}}$ of 
$p$ that divides 
$\#\text{GL}_{r}(\mathbb{F}_{p})$. The field 
$k_{T}$ that occurs in Theorem 1.1 is thus the compositum of 
$k(\unicode[STIX]{x1D707}_{p})$ and a Galois extension 
$k_{T}^{\prime }$ of 
$k$ in 
$k_{\unicode[STIX]{x1D6F4}}$ of exponent dividing 
$p^{i_{r}}$.
Write 
$k_{\unicode[STIX]{x1D6F4},r}^{\prime }$ for the compositum of the fields 
$k_{T}^{\prime }$ as 
$\unicode[STIX]{x1D70C}$ runs over all such representations. Then 
$k_{\unicode[STIX]{x1D6F4},r}^{\prime }$ is a Galois extension of 
$k$ in 
$k_{\unicode[STIX]{x1D6F4}}^{p}$ of exponent dividing 
$p^{i_{r}}$ and, since 
$G_{k_{\unicode[STIX]{x1D6F4}}^{p}/k}$ is topologically finitely generated, this implies 
$k_{\unicode[STIX]{x1D6F4},r}^{\prime }$ is a finite extension of 
$k$. We thus obtain a finite Galois extension of 
$k$ in 
$k_{\unicode[STIX]{x1D6F4}}$ by setting 
$k_{\unicode[STIX]{x1D6F4},r}:=k_{\unicode[STIX]{x1D6F4},r}^{\prime }(\unicode[STIX]{x1D707}_{p})$.
The proof of Theorem 1.1 shows that the same bounds on 
$\text{rk}_{p}(R_{F/E,T}^{i})$ and 
$\text{rk}_{p}(R_{F/E,T,c}^{i})$ are valid if one replaces 
$F_{T}$ with the larger field 
$F_{\unicode[STIX]{x1D6F4},r}:=k_{\unicode[STIX]{x1D6F4},r}F$. Hence, since the given bound on 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{\unicode[STIX]{x1D6F4},r}))+\#\unicode[STIX]{x1D6F4}_{f,F}$ implies a bound on both 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{\unicode[STIX]{x1D6F4},r}))$ and 
$\#\unicode[STIX]{x1D6F4}_{f,F}$, this argument gives a bound on the 
$\mathbb{Z}_{p}$-ranks of the lattices 
$R_{F/E,T,\text{tf}}^{i}$ and 
$R_{F/E,T,c,\text{tf}}^{i}$.
The claimed result now follows since, by the Jordan–Zassenhaus theorem [Reference Curtis and Reiner8, Theorem (24.2)], there are, up to isomorphism, only finitely many 
$\mathbb{Z}_{p}[{\mathcal{G}}]$-lattices of any given rank.◻
For a concrete arithmetical application of this result for the representations 
$T=\mathbb{Z}_{p}(r)$ for varying integers 
$r$, see Corollary 4.1 (and Proposition 4.2).
In general, the following example shows the bounds required by Corollary 3.1 arise in natural families of extensions.
In the sequel we write 
$E_{\text{cyc}}$ for the cyclotomic 
$\mathbb{Z}_{p}$-extension of a number field 
$E$.
Example 3.2. Assume 
$k$ contains 
$\unicode[STIX]{x1D707}_{p}$, fix a pro-
$p$ 
$p$-adic analytic extension 
$K$ of 
$k$ containing 
$k_{\text{cyc}}$ and unramified outside 
$\unicode[STIX]{x1D6F4}$ and set 
$E_{\unicode[STIX]{x1D6F4},r}:=k_{\unicode[STIX]{x1D6F4},r}E$ for each subfield 
$E$ of 
$K$. Fix a finite group 
${\mathcal{G}}$ of 
$p$-power order and a natural number 
$e$ and write 
$\text{Ext}({\mathcal{G}},K/k,e)$ for the family of Galois extensions 
$F/E$ with 
$G_{F/E}$ isomorphic to 
${\mathcal{G}}$, 
$k\subseteq E\subset F\subset K$, 
$E/k$ finite and 
$[E:E\cap k_{\text{cyc}}]\leqslant e$. For any such 
$F/E$ the degree over 
$k_{\text{cyc}}$ of the Galois closure of 
$F_{\text{cyc}}$ over 
$k_{\text{cyc}}$ is at most the maximal power 
$p^{m}$ of 
$p$ that divides 
$(e\#{\mathcal{G}})!$ In addition, since in this case 
$K_{\unicode[STIX]{x1D6F4},r}$ is a pro-
$p$ 
$p$-adic analytic extension of 
$k_{\text{cyc}}$, the compositum 
$K_{r,m}$ of 
$k_{\unicode[STIX]{x1D6F4},r}$ with the largest Galois extension of 
$k_{\text{cyc}}$ in 
$K$ of exponent dividing 
$p^{m}$ is of finite 
$p$-power degree over 
$k_{\text{cyc}}$. Now 
$(F_{\unicode[STIX]{x1D6F4},r})_{\text{cyc}}$ is one of the finitely many intermediate fields 
$L$ of 
$K_{r,m}/k_{\text{cyc}}$ and if the Iwasawa 
$\unicode[STIX]{x1D707}$-invariant of 
$k_{\text{cyc}}$ vanishes (as conjectured by Iwasawa [Reference Iwasawa14]) one can show 
$G_{L_{\unicode[STIX]{x1D6F4}}^{p,\text{ab}}/L}$ is a finitely generated 
$\mathbb{Z}_{p}$-module for each such 
$L$. By using [Reference Washington20, Proposition 13.23] this gives a finite upper bound on 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{\unicode[STIX]{x1D6F4},r}))$ that depends only on 
$K_{r,m}/k$. Since every place in 
$\unicode[STIX]{x1D6F4}_{f}$ is only finitely decomposed in 
$K_{r,m}/k$ one can also give a similar bound on 
$\#\unicode[STIX]{x1D6F4}_{f,F}$ and so Corollary 3.1 applies to the family 
$\text{Ext}({\mathcal{G}},K/k,e)$.
3.2
In this section we prove Corollary 1.2. To do so we first recall details concerning the finite support cohomology and Selmer groups introduced by Bloch and Kato.
With 
${\mathcal{F}}$ denoting either 
$T$ or 
$W:=(\mathbb{Q}_{p}/\mathbb{Z}_{p})\otimes _{\mathbb{Z}_{p}}T$, for each place 
$w$ of each finite extension 
$L$ of 
$k$ in 
$k^{c}$ we write 
$H_{f}^{1}(L_{w},{\mathcal{F}})$ for the “finite support cohomology” subgroup of 
$H^{1}(L_{w},{\mathcal{F}})$ defined in [Reference Bloch and Kato2]. Then the Bloch–Kato Selmer group 
$\text{Sel}_{L}(W)$ of 
$W$ over 
$L$ is defined to be the kernel of the natural diagonal localization map
$$\begin{eqnarray}\displaystyle H^{1}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}},W)\rightarrow \mathop{\bigoplus }_{w\in \unicode[STIX]{x1D6F4}_{L}}\frac{H^{1}(L_{w},W)}{H_{f}^{1}(L_{w},W)}. & & \displaystyle \nonumber\end{eqnarray}$$ Setting 
$\text{Sel}_{L}(T):=\text{Sel}_{L}(W)^{\vee }$, Artin–Verdier duality gives rise (via, for example, the computations of [Reference Burns and Flach4, pp. 86–87]) to an exact sequence of finitely generated 
$\mathbb{Z}_{p}$-modules
$$\begin{eqnarray}\mathop{\bigoplus }_{w\in \unicode[STIX]{x1D6F4}_{f,L}}H_{f}^{1}(L_{w},T)\rightarrow H_{c}^{2}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}},T)\rightarrow \text{Sel}_{L}(T)\rightarrow 0\end{eqnarray}$$and hence to an inequality
$$\begin{eqnarray}\displaystyle \text{rk}(H_{c}^{2}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}},T))-\mathop{\sum }_{w\in \unicode[STIX]{x1D6F4}_{f,L}}\text{rk}(H_{f}^{1}(L_{w},T)) & {\leqslant} & \displaystyle \text{rk}(\text{Sel}_{L}(T))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \text{rk}(H_{c}^{2}({\mathcal{O}}_{L,\unicode[STIX]{x1D6F4}},T)).\end{eqnarray}$$ It is also well known that for each 
$w\in \unicode[STIX]{x1D6F4}_{f,L}$ one has
$$\begin{eqnarray}\displaystyle \text{rk}(H_{f}^{1}(L_{w},T))\leqslant \left\{\begin{array}{@{}ll@{}}\text{rk}(T)([L_{w}:\mathbb{Q}_{p}]+1)\quad & \text{if}~w\text{ is }p\text{-}\text{adic},\\ \text{rk}(T)\quad & \text{otherwise}\end{array}\right. & & \displaystyle\end{eqnarray}$$ (for example, this follows directly from [Reference Burns and Flach4, (1.5) and (1.7)] and the fact that if 
$w$ is 
$p$-adic, then the 
$\mathbb{Q}_{p}$-dimension of the tangent space of 
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}T$ over 
$L_{w}$ is at most 
$[L_{w}:\mathbb{Q}_{p}]\cdot \text{rk}(T)$).
Turning to the proof of Corollary 1.2 we assume the notation and hypotheses of that result, we set 
$G:=G_{F/E}$ and we fix a decomposition 
$H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)=P_{F/E,T,c}^{2}\oplus R_{F/E,T,c}^{2}$ of the form stated in Theorem 1.1.
As 
$G$ is here assumed to be a 
$p$-group, the 
$\mathbb{Z}_{p}[G]$-module 
$P_{F/E,T,c}^{2}$ is free and so one has 
$\text{rk}(P_{F/E,T,c}^{2})=\#G\cdot \text{rk}(H^{0}(G,P_{F/E,T,c}^{2}))$. In addition, since the isomorphism in Proposition 2.3(i) induces an identification of 
$\mathbb{Q}_{p}$-spaces 
$H^{0}(G,\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T))\cong \mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}H_{c}^{2}({\mathcal{O}}_{E,\unicode[STIX]{x1D6F4}},T)$, one has
$$\begin{eqnarray}\displaystyle \text{rk}(H^{0}(G,P_{F/E,T,c}^{2})) & = & \displaystyle \text{rk}(H^{0}(G,H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T)))-\text{rk}(H^{0}(G,R_{F/E,T,c}^{2}))\nonumber\\ \displaystyle & = & \displaystyle \text{rk}(H_{c}^{2}({\mathcal{O}}_{E,\unicode[STIX]{x1D6F4}},T))-\text{rk}(H^{0}(G,R_{F/E,T,c}^{2}))\nonumber\end{eqnarray}$$and hence
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{rk}(H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T))\nonumber\\ \displaystyle & & \displaystyle \quad =\text{rk}(P_{F/E,T,c}^{2})+\text{rk}(R_{F/E,T,c}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\#G\cdot \text{rk}(H^{0}(G,P_{F/E,T,c}^{2}))+\text{rk}(R_{F/E,T,c}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\#G(\text{rk}(H_{c}^{2}({\mathcal{O}}_{E,\unicode[STIX]{x1D6F4}},T))-\text{rk}(H^{0}(G,R_{F/E,T,c}^{2})))+\text{rk}(R_{F/E,T,c}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\#G\cdot \text{rk}(H_{c}^{2}({\mathcal{O}}_{E,\unicode[STIX]{x1D6F4}},T))+\unicode[STIX]{x1D6FF}_{F/E,T}\nonumber\end{eqnarray}$$ with 
$\unicode[STIX]{x1D6FF}_{F/E,T}:=\text{rk}(R_{F/E,T,c}^{2})-\#G\cdot \text{rk}(H^{0}(G,R_{F/E,T,c}^{2}))$ so that
$$\begin{eqnarray}\displaystyle -\#G\cdot \text{rk}_{p}(R_{F/E,T,c,\text{tf}}^{2})\leqslant \unicode[STIX]{x1D6FF}_{F/E,T}\leqslant \text{rk}_{p}(R_{F/E,T,c,\text{tf}}^{2}). & & \displaystyle \nonumber\end{eqnarray}$$ These facts combine with (14) and (15) (for both 
$L=F$ and 
$L=E$) to give inequalities
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{rk}(\text{Sel}_{F}(T))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \text{rk}(H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T))=\#G\cdot \text{rk}(H_{c}^{2}({\mathcal{O}}_{E,\unicode[STIX]{x1D6F4}},T))+\unicode[STIX]{x1D6FF}_{F/E,T}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \#G(\text{rk}(\text{Sel}_{E}(T))+\text{rk}(T)(\#\unicode[STIX]{x1D6F4}_{f,E}+[E:\mathbb{Q}]))+\unicode[STIX]{x1D6FF}_{F/E,T}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \#G\cdot \text{rk}(\text{Sel}_{E}(T))+\text{rk}(T)(\#G\cdot \#\unicode[STIX]{x1D6F4}_{f,F}+[F:\mathbb{Q}])+\text{rk}_{p}(R_{F/E,T,c,\text{tf}}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \#G\cdot \text{rk}(\text{Sel}_{E}(T))+r(\#G\cdot \#\unicode[STIX]{x1D6F4}_{f,F}+[F:\mathbb{Q}])+\text{rk}_{p}(R_{F/E,T,c,\text{tf}}^{2})\nonumber\end{eqnarray}$$and
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{rk}(\text{Sel}_{F}(T))\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \text{rk}(H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},T))-\text{rk}(T)(\#\unicode[STIX]{x1D6F4}_{f,F}+[F:\mathbb{Q}])\nonumber\\ \displaystyle & & \displaystyle \quad =\#G\cdot \text{rk}(H_{c}^{2}({\mathcal{O}}_{E,\unicode[STIX]{x1D6F4}},T))+\unicode[STIX]{x1D6FF}_{F/E,T}-\text{rk}(T)(\#\unicode[STIX]{x1D6F4}_{f,F}+[F:\mathbb{Q}])\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \#G\cdot \text{rk}(\text{Sel}_{E}(T))-\text{rk}(T)(\#\unicode[STIX]{x1D6F4}_{f,F}+[F:\mathbb{Q}])-\#G\cdot \text{rk}_{p}(R_{F/E,T,c,\text{tf}}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \#G\cdot \text{rk}(\text{Sel}_{E}(T))-r(\#\unicode[STIX]{x1D6F4}_{f,F}+[F:\mathbb{Q}])-\#G\cdot \text{rk}_{p}(R_{F/E,T,c,\text{tf}}^{2}).\nonumber\end{eqnarray}$$ To deduce Corollary 1.2 from these explicit inequalities it is enough to note the argument of Corollary 3.1 gives an upper bound on 
$\text{rk}_{p}(R_{F/E,T,c,\text{tf}}^{2})$ that depends only on 
$\#G$, 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(k_{\unicode[STIX]{x1D6F4},r}F))$ and 
$\#\unicode[STIX]{x1D6F4}_{f,F}$.
4 The representations $T=\mathbb{Z}_{p}(r)$
By means of concrete arithmetic examples, in this section we explore consequences of Theorem 1.1 for the representations 
$T=\mathbb{Z}_{p}(r)$ for varying integers 
$r$.
We also show that in this context, and for special classes of extensions 
$F/E$, our methods can lead to very explicit structural results.
4.1
We first record a general consequence of Corollary 3.1 in this case.
For any abstract finite group 
${\mathcal{G}}$, any finite set of rational places 
$\unicode[STIX]{x1D6F4}$ that contains 
$p$ and any natural number 
$b$ we write 
$\text{Ext}({\mathcal{G}},\unicode[STIX]{x1D6F4},b)$ for the family of Galois extensions of number fields 
$F/E$ that satisfy all of the following properties
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}G_{F/E}\text{ is isomorphic to }{\mathcal{G}},\quad \\ E\text{ contains }\unicode[STIX]{x1D707}_{p},\quad \\ F/E\text{ is unramified outside }\unicode[STIX]{x1D6F4}_{E},\quad \\ \text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F))+\#\unicode[STIX]{x1D6F4}_{f,F}\leqslant b.\quad \end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$Then Corollary 3.1 has the following concrete consequence concerning Galois structures in these families.
Corollary 4.1. Fix data 
${\mathcal{G}}$, 
$\unicode[STIX]{x1D6F4}$ and 
$b$ as above. Then, as the extension 
$F/E$ ranges over 
$\text{Ext}({\mathcal{G}},\unicode[STIX]{x1D6F4},b)$ there are, up to projective direct summands, only finitely many isomorphism classes of 
$\mathbb{Z}_{p}[{\mathcal{G}}]$-modules arising from either 
$\text{Gal}(F_{\unicode[STIX]{x1D6F4}}^{p,\text{ab}}/F)_{\text{tf}}$ or 
$(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}))_{\text{tf}}$ for any nonnegative integer 
$a$.
Proof. If 
$T=\mathbb{Z}_{p}(a)$ for any integer 
$a$, then the associated 
$p$-adic representation of 
$G_{\mathbb{Q}(\unicode[STIX]{x1D707}_{p}),\unicode[STIX]{x1D6F4}}$ has pro-
$p$ image and for every field 
$F$ as above one has 
$F_{T}=F$.
The claimed result thus follows directly from the proof of Corollary 3.1 (with 
$k$ replaced by 
$\mathbb{Q}(\unicode[STIX]{x1D707}_{p})$) and the fact that there are canonical isomorphisms of 
$\mathbb{Z}_{p}[G_{F/E}]$-modules
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}H^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},\mathbb{Z}_{p}(1))\cong \mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}^{\times }=\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}),\quad \\ H^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},\mathbb{Z}_{p}(1+a))\cong \mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}})\,\,\text{ for }\,\,a>0,\quad \\ H_{c}^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},\mathbb{Z}_{p}(1))\cong \text{Gal}(F_{\unicode[STIX]{x1D6F4}}^{p,\text{ab}}/F).\quad \end{array}\right. & & \displaystyle\end{eqnarray}$$Here the first isomorphism is induced by Kummer theory, the second by the fact that the Chern class homomorphism
$$\begin{eqnarray}\displaystyle \mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}})\rightarrow H^{1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},\mathbb{Z}_{p}(1+a)) & & \displaystyle \nonumber\end{eqnarray}$$is bijective (by the known validity of the Quillen–Lichtenbaum conjecture – see Weibel [Reference Weibel21]) and the third by the Artin–Verdier duality theorem. ◻
In the sequel, for each natural number 
$m$ and each number field 
$E$ we shall write 
$E^{m}$ for the field generated over 
$E$ by a primitive 
$p^{m}$th root of unity.
The interest of Corollary 4.1 is explained by the following result.
Proposition 4.2. Let 
${\mathcal{G}}$ be a finite group of odd order that has a commutator subgroup of 
$p$-power order. Then for any large enough finite set of rational places 
$\unicode[STIX]{x1D6F4}$ and any large enough integer 
$b$ the 
$\mathbb{Z}_{p}$-rank of 
$\text{Gal}(F_{\unicode[STIX]{x1D6F4}}^{p,\text{ab}}/F)_{\text{tf}}$, and of 
$(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}))_{\text{tf}}$ for any nonnegative integer 
$a$, is unbounded as 
$F/E$ ranges over 
$\text{Ext}({\mathcal{G}},\unicode[STIX]{x1D6F4},b)$.
Proof. As any such group 
${\mathcal{G}}$ is both solvable and of order prime to the number of roots of unity in 
$\mathbb{Q}$ there exists a Galois extension 
$F$ of 
$\mathbb{Q}$ for which 
$G_{F/\mathbb{Q}}$ is isomorphic to 
${\mathcal{G}}$ and 
$p$ is unramified in 
$F$ (see Neukirch [Reference Neukirch17, Corollary 2, p. 156]). We write 
$\unicode[STIX]{x1D6F4}$ for the set of rational places comprising 
$\infty ,p$ and those primes that ramify in 
$F/\mathbb{Q}$.
We claim that for any large enough integer 
$b$, all of the extensions 
$F^{m}/\mathbb{Q}^{m}$ as 
$m$ varies belong to 
$\text{Ext}({\mathcal{G}},\unicode[STIX]{x1D6F4},b)$.
At the outset it is clear 
$\mathbb{Q}^{m}$ contains 
$\unicode[STIX]{x1D707}_{p}$, 
$F^{m}/\mathbb{Q}^{m}$ is unramified outside 
$\unicode[STIX]{x1D6F4}$ and, as 
$\mathbb{Q}^{m}/\mathbb{Q}$ is disjoint from 
$F/\mathbb{Q}$ (since 
$p$ is unramified in 
$F$), 
$G_{F^{m}/\mathbb{Q}^{m}}$ is isomorphic to 
${\mathcal{G}}$.
We next write 
$F^{\infty }$ for the union of the fields 
$F^{m}$ for 
$m>0$. Then each rational prime has open decomposition group in 
$G_{F^{\infty }/\mathbb{Q}}$ and so 
$\#\unicode[STIX]{x1D6F4}_{f,F^{m}}$ is bounded independently of 
$m$. In addition, since 
$F^{1}$ is (by our assumption on the commutator subgroup of 
${\mathcal{G}}$) a Galois extension of 
$p$-power degree of an abelian field, the Iwasawa 
$\unicode[STIX]{x1D707}$-invariant of 
$F^{\infty }/F^{1}$ vanishes and so 
$\text{rk}_{p}(\text{Cl}_{\unicode[STIX]{x1D6F4}}(F^{m}))$ is bounded independently of 
$m$ (by [Reference Washington20, Proposition 13.23]).
At this stage we know that, for any sufficiently large integer 
$b$, the extensions 
$F^{m}/\mathbb{Q}^{m}$ all belong to 
$\text{Ext}({\mathcal{G}},\unicode[STIX]{x1D6F4},b)$. It is thus enough to note that, since the number of complex places of 
$F^{m}$ is 
$[F^{m}:\mathbb{Q}]/2$, one has 
$\text{rk}(\text{Gal}((F^{m})_{\unicode[STIX]{x1D6F4}}^{p,\text{ab}}/F^{m})_{\text{tf}})\geqslant [F^{m}:\mathbb{Q}]/2-1$ and, for any nonnegative integer 
$a$, also 
$\text{rk}((\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F^{m},\unicode[STIX]{x1D6F4}}))_{\text{tf}})\geqslant [F^{m}:\mathbb{Q}]/2$.◻
4.2
In this section we explain how techniques developed in [Reference Burns, Macias Castillo and Wuthrich7] can be used to make the structure results of Corollary 4.1 more precise in the case of cyclic extensions of 
$p$-power degree. We thus fix such an extension 
$F/k$, set 
$G:=G_{F/k}$ and 
$[F:k]=p^{n}$ and for each integer 
$i$ with 
$0\leqslant i\leqslant n$, let 
$F_{i}$ denote the unique extension of 
$k$ in 
$F$ of degree 
$p^{i}$.
For any nonnegative integer 
$a$ and intermediate field 
$F_{i}$ of 
$F/k$ we write 
$\text{cap}_{F,i,\unicode[STIX]{x1D6F4}}^{a}$ for the “
$p$-primary capitulation kernel”
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}ll@{}}\mathbb{Z}_{p}\otimes _{\mathbb{Z}}\ker (\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{i})\rightarrow \text{Cl}_{\unicode[STIX]{x1D6F4}}(F))\quad & \text{if}~a=0,\\ \mathbb{Z}_{p}\otimes _{\mathbb{Z}}\ker (K_{2a}({\mathcal{O}}_{F_{i},\unicode[STIX]{x1D6F4}})\rightarrow K_{2a}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}))\quad & \text{if}~a>0\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$ where the arrows denote the respective homomorphisms that are induced by the ring inclusion 
${\mathcal{O}}_{F_{i},\unicode[STIX]{x1D6F4}}\subseteq {\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}$.
We write 
$r_{1,E}$ and 
$r_{2,E}$ for the number of real and complex places of a number field 
$E$.
Theorem 4.3. Fix a nonnegative integer 
$a$ for which the cohomology group 
$H^{0}(G_{k,\unicode[STIX]{x1D6F4}},(\mathbb{Q}_{p}/\mathbb{Z}_{p})(1+a))$ vanishes.
Then the isomorphism class of the 
$\mathbb{Z}_{p}[G]$-module 
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}})$ is uniquely determined (in the sense described in [Reference Burns, Macias Castillo and Wuthrich7, Section 3.2.1]) by the diagram
$$\begin{eqnarray}\displaystyle \text{cap}_{F,0,\unicode[STIX]{x1D6F4}}^{a}\leftrightarrows \text{cap}_{F,1,\unicode[STIX]{x1D6F4}}^{a}\leftrightarrows \cdots \leftrightarrows \text{cap}_{F,n-1,\unicode[STIX]{x1D6F4}}^{a}, & & \displaystyle\end{eqnarray}$$ where the upper and lower arrows are the homomorphisms induced by the field-theoretic norms 
$F_{i+1}^{\times }\rightarrow F_{i}^{\times }$ and inclusions 
${\mathcal{O}}_{F_{i},\unicode[STIX]{x1D6F4}}\subseteq {\mathcal{O}}_{F_{i+1},\unicode[STIX]{x1D6F4}}$, respectively, together with knowledge of
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}ll@{}}\#\unicode[STIX]{x1D6F4}_{F_{i}}~\text{for each}~i~\text{with}~0\leqslant i\leqslant n\quad & \text{if}~a=0,\\ r_{2,k}\quad & \text{if}~a>0~\text{and}~a~\text{is odd},\\ r_{1,k}+r_{2,k}\quad & \text{if}~a>0~\text{and}~a~\text{is even}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$Proof. Fix a nonnegative integer 
$a$ and an integer 
$i$ with 
$0\,\leqslant \,i\,\leqslant \,n$. Then the assumed vanishing of the group 
$H^{0}(G_{k,\unicode[STIX]{x1D6F4}},(\mathbb{Q}_{p}/\mathbb{Z}_{p})(1+a))$ implies that 
$H^{0}(G_{F_{i},\unicode[STIX]{x1D6F4}},(\mathbb{Q}_{p}/\mathbb{Z}_{p})(1+a))$ also vanishes. This in turn implies that the module 
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}})$ is 
$\mathbb{Z}_{p}$-free and also combines with the description of Proposition 2.3(ii), the exact sequence (6) and the isomorphisms 
$H^{2}({\mathcal{O}}_{F_{i},\unicode[STIX]{x1D6F4}},\mathbb{Z}_{p}(1))_{\text{tor}}\cong \mathbb{Z}_{p}\otimes _{\mathbb{Z}}\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{i})$ and 
$H^{2}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}},\mathbb{Z}_{p}(1+a))\cong \mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}})$ for 
$a>0$ that are respectively induced by class field theory and the canonical Chern class homomorphism, to imply that the complex 
$C_{i}(a):=R\unicode[STIX]{x1D6E4}_{c}({\mathcal{O}}_{F_{i},\unicode[STIX]{x1D6F4}},\mathbb{Z}_{p}(-a))$ is acyclic outside one and two and is such that there is a canonical short exact sequence
$$\begin{eqnarray}\displaystyle 0\rightarrow B_{i}^{a}\rightarrow H^{2}(C_{i}(a))\rightarrow (\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F_{i},\unicode[STIX]{x1D6F4}}))^{\ast }\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ with 
$B_{i}^{0}:=(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}\text{Cl}_{\unicode[STIX]{x1D6F4}}(F_{i}))^{\vee }$ and 
$B_{i}^{a}:=(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}))^{\vee }$ for 
$a>0$. In addition, since 
$C_{i}(a)$ is acyclic in degrees greater than two the descent isomorphism 
$\mathbb{Z}_{p}[G_{F_{i}/k}]\otimes _{\mathbb{Z}_{p}[G]}^{\mathbb{L}}C_{n}(a)\cong C_{i}(a)$ from Proposition 2.3(i) induces an identification 
$H_{0}(G_{F/F_{i}},H^{2}(C_{n}(a)))\cong H^{2}(C_{i}(a))$.
Given these facts, one can simply follow the argument of [Reference Burns, Macias Castillo and Wuthrich7, Section 3.2.1] (with the terms 
$\overline{X}$ and 
that occur in that argument being respectively replaced by 
$(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}))^{\ast }$ and 
$B_{i}^{a}$) to deduce that the isomorphism class of the 
$\mathbb{Z}_{p}[G]$-lattice 
$(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}))^{\ast }$, and hence also of 
$(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}}))_{\text{tf}}=\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}})$, is uniquely determined, in a sense that is made precise in [Reference Burns, Macias Castillo and Wuthrich7, Lemma 3.5], by the (Pontryagin dual of the) diagram (17) together with knowledge of the rank 
$r_{i}^{a}:=\text{rk}(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F_{i},\unicode[STIX]{x1D6F4}}))$ for each 
$i$.
The claimed result thus follows from the fact that for each 
$i$ one has 
$r_{i}^{0}=\#\unicode[STIX]{x1D6F4}_{F_{i}}-1$ and if 
$a>0$ is odd, respectively even, also 
$r_{i}^{a}=r_{2,F_{i}}=p^{i}\cdot r_{2,k}$, respectively 
$r_{i}^{a}=r_{1,F_{i}}+r_{2,F_{i}}=p^{i}(r_{1,k}+r_{2,k})$.◻
Remark 4.4. An important special case of Theorem 4.3 arises when 
$\text{cap}_{F,i,\unicode[STIX]{x1D6F4}}^{a}$ vanishes for each 
$i$ with 
$0\leqslant i<n$. In this case a closer analysis of the argument in [Reference Burns, Macias Castillo and Wuthrich7, Section 3.2.1] shows that 
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}K_{2a+1}({\mathcal{O}}_{F,\unicode[STIX]{x1D6F4}})$ is a free 
$\mathbb{Z}_{p}[G]$-module if 
$a>0$ and is isomorphic to the direct sum 
$\bigoplus _{j=0}^{j=n}\mathbb{Z}_{p}[G_{F_{j}/k}]^{m_{j}}$ if 
$a=0$, where the nonnegative integers 
$m_{j}$ are determined by the equalities 
$\sum _{j=0}^{j=n}m_{j}\cdot p^{\text{min}\{j,b\}}=\#\unicode[STIX]{x1D6F4}_{F_{b}}-1$ for each 
$b$ with 
$0\leqslant b\leqslant n$.
4.3
In this final section we show that, in special cases, our approach can be used to make the result of Theorem 4.3 much more explicit.
To do this we fix an odd prime 
$p$ and for each number field 
$k$ and nonnegative integer 
$n$ write 
$k_{n}$ for the unique subfield of 
$k_{\text{cyc}}$ that has degree 
$p^{n}$ over 
$k$. For each such 
$n$ we also fix a primitive 
$p^{n}$th root of unity 
$\unicode[STIX]{x1D701}_{n}$ in 
$\mathbb{Q}^{c}$ with 
$\unicode[STIX]{x1D701}_{n}^{p}=\unicode[STIX]{x1D701}_{n-1}$.
We assume throughout that the following hypothesis is satisfied.
Hypothesis 4.5. 
$k$ is disjoint from 
$\mathbb{Q}_{\text{cyc}}$ and does not contain a 
$p$th root of 
$\unicode[STIX]{x1D714}\cdot p$ for any root of unity 
$\unicode[STIX]{x1D714}$.
Remark 4.6. This hypothesis is satisfied if, for example, the absolute ramification index of some 
$p$-adic place of 
$k$ is prime to 
$p$.
We write 
$\unicode[STIX]{x1D6F4}$ for the set of places of 
$k$ that are either archimedean or 
$p$-adic and for each 
$n$ we study the structure of the 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$-module 
$H^{1}({\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}},\mathbb{Z}_{p}(1))\cong \mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times }$.
To do this we define an element of 
${\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times }$ by setting
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}_{n}:=\text{Norm}_{\mathbb{Q}^{n+1}/\mathbb{Q}_{n}}(\unicode[STIX]{x1D701}_{n+1}-1). & & \displaystyle \nonumber\end{eqnarray}$$Proposition 4.7. Let 
$k$ be any number field satisfying Hypothesis 4.5. Then for each natural number 
$n$ the element 
$\unicode[STIX]{x1D716}_{n}$ generates a 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$-submodule of 
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times }$ that is both a direct summand and isomorphic to 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$.
Proof. The fact that 
$k$ is disjoint from 
$\mathbb{Q}_{\text{cyc}}$ implies that the restriction map 
$G_{k_{n}/k}\rightarrow G_{\mathbb{Q}_{n}/\mathbb{Q}}$ is bijective and hence that
$$\begin{eqnarray}\displaystyle \text{Norm}_{k_{n}/k}(\unicode[STIX]{x1D716}_{n})=\text{Norm}_{\mathbb{Q}_{n}/\mathbb{Q}}(\unicode[STIX]{x1D716}_{n})=\text{Norm}_{\mathbb{Q}^{n+1}/\mathbb{Q}}(\unicode[STIX]{x1D701}_{n+1}-1)=p. & & \displaystyle \nonumber\end{eqnarray}$$ Since 
$k$ does not contain a 
$p$th root of 
$\unicode[STIX]{x1D714}\cdot p$ for any root of unity 
$\unicode[STIX]{x1D714}$, this equality implies the image 
$\unicode[STIX]{x1D716}_{n,p}^{0}$ of 
$\text{Norm}_{k_{n}/k}(\unicode[STIX]{x1D716}_{n})$ in the lattice 
$(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k,\unicode[STIX]{x1D6F4}}^{\times })_{\text{tf}}$ is not divisible by 
$p$.
We set 
$\unicode[STIX]{x1D6E4}_{n}:=G_{k_{n}/k}$, 
$U_{n,p}:=\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times }$ and 
$\unicode[STIX]{x1D707}_{n,p}:=(U_{n,p})_{\text{tor}}$. Then by applying the functor 
$H^{0}(\unicode[STIX]{x1D6E4}_{n},-)$ to the tautological exact sequence
$$\begin{eqnarray}\displaystyle 1\rightarrow \unicode[STIX]{x1D707}_{n,p}\rightarrow U_{n,p}\rightarrow (U_{n,p})_{\text{tf}}\rightarrow 1 & & \displaystyle \nonumber\end{eqnarray}$$one obtains an exact sequence of abelian groups
$$\begin{eqnarray}\displaystyle 0\rightarrow (\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k,\unicode[STIX]{x1D6F4}}^{\times })_{\text{tf}}\xrightarrow[{}]{\unicode[STIX]{x1D704}_{n,p}}H^{0}(\unicode[STIX]{x1D6E4}_{n},(U_{n,p})_{\text{tf}})\rightarrow H^{1}(\unicode[STIX]{x1D6E4}_{n},\unicode[STIX]{x1D707}_{n,p}). & & \displaystyle \nonumber\end{eqnarray}$$ Let us assume for the moment that the group 
$H^{1}(\unicode[STIX]{x1D6E4}_{n},\unicode[STIX]{x1D707}_{n,p})$ vanishes. Then this sequence shows that 
$\unicode[STIX]{x1D704}_{n,p}$ is bijective and so the above considerations imply that the image 
$\unicode[STIX]{x1D716}_{n,p}$ of 
$\unicode[STIX]{x1D716}_{n}$ in 
$(U_{n,p})_{\text{tf}}$ is such that 
$\text{tr}_{\unicode[STIX]{x1D6E4}_{n}}(\unicode[STIX]{x1D716}_{n,p})=\unicode[STIX]{x1D704}_{n,p}(\unicode[STIX]{x1D716}_{n,p}^{0})$ is not divisible by 
$p$ in 
$H^{0}(\unicode[STIX]{x1D6E4}_{n},(U_{n,p})_{\text{tf}})$. Given this, we can apply Proposition 2.1 to the data 
$G=\unicode[STIX]{x1D6E4}_{n},X=(U_{n,p})_{\text{tf}},t=1$ and 
$x_{1}=\unicode[STIX]{x1D716}_{n,p}$ to deduce that 
$\unicode[STIX]{x1D716}_{n,p}$ generates a 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$-submodule of 
$(U_{n,p})_{\text{tf}}$ that is both a direct summand and isomorphic to 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$. It is then clear that 
$\unicode[STIX]{x1D716}_{n}$ generates a 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$-submodule of 
$U_{n,p}$ that is a direct summand and isomorphic to 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$, as claimed.
It therefore suffices to check 
$H^{1}(\unicode[STIX]{x1D6E4}_{n},\unicode[STIX]{x1D707}_{n,p})$ vanishes and this is clear if 
$k$ does not contain 
$\unicode[STIX]{x1D701}_{1}$ since then the group 
$\unicode[STIX]{x1D707}_{n,p}$ vanishes.
If, on the other hand, 
$k$ contains 
$\unicode[STIX]{x1D701}_{1}$, then (as 
$k$ is disjoint from 
$\mathbb{Q}_{\text{cyc}}$) the torsion subgroup 
$H^{0}(\unicode[STIX]{x1D6E4}_{n},\unicode[STIX]{x1D707}_{n,p})$ of 
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k,\unicode[STIX]{x1D6F4}}^{\times }$ is generated by 
$\unicode[STIX]{x1D701}_{1}$ and the group 
$\unicode[STIX]{x1D707}_{n,p}$ by 
$\unicode[STIX]{x1D701}_{n+1}$. Since 
$\text{Norm}_{k_{n}/k}(\unicode[STIX]{x1D701}_{n+1})=\unicode[STIX]{x1D701}_{1}$ this shows that the Tate cohomology group 
${\hat{H}}^{0}(\unicode[STIX]{x1D6E4}_{n},\unicode[STIX]{x1D707}_{n,p})$ vanishes, and hence also (since 
$\unicode[STIX]{x1D6E4}_{n}$ is cyclic) that the group 
$H^{1}(\unicode[STIX]{x1D6E4}_{n},\unicode[STIX]{x1D707}_{n,p})$ vanishes, as required.◻
This result implies some very explicit structural results. To explain this we start with an easy special case.
Corollary 4.8. Let 
$k$ be either 
$\mathbb{Q}$ or an imaginary quadratic field in which 
$p$ is not split. Then for each natural number 
$n$ the 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$-module 
$(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times })_{\text{tf}}$ is free of rank one.
Proof. The stated conditions on 
$k$ imply that it satisfies Hypothesis 4.5 and in addition that 
$k_{n}$ has 
$p^{n}$ archimedean places and a unique 
$p$-adic place and hence that 
$\text{rk}(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times })$ is equal to 
$(p^{n}-1)+1=\text{rk}(\mathbb{Z}_{p}[G_{k_{n}/k}])$. In these cases, therefore, the result of Proposition 4.7 implies 
$(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times })_{\text{tf}}$ is equal to 
$\mathbb{Z}_{p}[G_{k_{n}/k}]\cdot \unicode[STIX]{x1D716}_{n,p}$ and so is a free 
$\mathbb{Z}_{p}[G_{k_{n}/k}]$-module of rank one.◻
In the rest of this section we consider the next simplest case by assuming that 
$k$ is a real quadratic field in which 
$p$ is inert.
In this case 
$k$ satisfies Hypothesis 4.5 and 
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times }$ is a free 
$\mathbb{Z}_{p}$-module of rank 
$2p^{n}$ so that Proposition 4.7 implies there is an isomorphism of 
$\mathbb{Z}_{p}[k_{n}/k]$-modules
$$\begin{eqnarray}\displaystyle \mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{n},\unicode[STIX]{x1D6F4}}^{\times }\cong \mathbb{Z}_{p}[G_{k_{n}/k}]\oplus V_{k_{n}/k} & & \displaystyle\end{eqnarray}$$ with 
$\text{rk}(V_{k_{n}/k})=p^{n}$.
For each pair of integers 
$i$ and 
$j$ with 
$0\leqslant i\leqslant j\leqslant n$ we now write
$$\begin{eqnarray}\displaystyle \text{cap}_{k_{i},p}^{k_{j}}:=\mathbb{Z}_{p}\otimes _{\mathbb{Z}}\ker (\text{Cl}(k_{i})\rightarrow \text{Cl}(k_{j})) & & \displaystyle \nonumber\end{eqnarray}$$ for the 
$p$-primary part of the kernel of the classical “capitulation” map on ideal classes. Then, in terms of the notation in Theorem 4.3, for all such 
$i$ and 
$j$ there are natural isomorphisms
$$\begin{eqnarray}\displaystyle {\hat{H}}^{-1}(G_{k_{j}/k_{i}},V_{k_{j}/k}^{\ast }) & \cong & \displaystyle {\hat{H}}^{-1}(G_{k_{j}/k_{i}},(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{j},\unicode[STIX]{x1D6F4}}^{\times })^{\ast })\nonumber\\ \displaystyle & \cong & \displaystyle (\text{cap}_{k_{j},i,\unicode[STIX]{x1D6F4}}^{0})^{\vee }\cong (\text{cap}_{k_{i},p}^{k_{j}})^{\vee }\end{eqnarray}$$ where the first follows directly from the 
$\mathbb{Z}_{p}$-linear dual of the isomorphism (18) (with 
$n$ replaced by 
$j$), the second from the argument of [Reference Burns, Macias Castillo and Wuthrich7, Proposition 3.1] (modified as per the 
$a=0$ case of the proof of Theorem 4.3) and the third follows trivially from the fact that 
$p$ is inert in 
$k$ and so the unique prime ideals of 
$k_{i}$ and 
$k_{j}$ above 
$p$ are principal.
To further analyse the structure of 
$V_{k_{n}/k}$ we now restrict to the case 
$n=2$ and use the Heller–Reiner classification of indecomposable 
$\mathbb{Z}_{p}[G_{k_{2}/k}]$-lattices from [Reference Heller and Reiner12]. In fact, for our purposes, the relevant properties of these lattices are conveniently displayed in [Reference Rzedowski-Calderón, Villa Salvador and Madan18, Table 2] and so in the following result we shall use the same notation for indecomposable lattices as in that table.
Corollary 4.9. Let 
$k$ be a real quadratic field in which 
$p$ is inert. Set 
$G:=G_{k_{2}/k}$ and write 
$Q$ for the quotient of 
$G$ of order 
$p$ and 
$Z_{p}$ for the set of integers 
$i$ with 
$1\leqslant i\leqslant p-2$. For integers 
$a$ and 
$b$ in 
$\{0,1,2\}$ with 
$a\leqslant b$ abbreviate 
$\text{cap}_{k_{a},p}^{k_{b}}$ to 
$\text{cap}_{a}^{b}$.
Then there is an isomorphism of 
$\mathbb{Z}_{p}[G]$-lattices 
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{2},\unicode[STIX]{x1D6F4}}^{\times }\cong \mathbb{Z}_{p}[G]\oplus V^{\ast }$ where the lattice 
$V$ is such that precisely one of the following cases arises.
$\text{(i)}~~~V=(R_{2},R_{1}\oplus \mathbb{Z}_{p},1\oplus 1)$ and 
$|\text{cap}_{0}^{1}|=|\text{cap}_{0}^{2}|=|\text{cap}_{1}^{2}|=p$.
$\text{(i)}_{i}~~V=(R_{2},R_{1}\oplus \mathbb{Z}_{p},1\oplus \unicode[STIX]{x1D706}_{0}^{i})$ with 
$i\in Z_{p}$, 
$|\text{cap}_{0}^{1}|=|\text{cap}_{0}^{2}|=p$ and 
$|\text{cap}_{1}^{2}|=p^{i}$.
$\text{(ii)}~~V=\mathbb{Z}_{p}[G]$ and 
$|\text{cap}_{0}^{1}|=|\text{cap}_{0}^{2}|=|\text{cap}_{1}^{2}|=1$.
$\text{(ii)}_{i}~V=(R_{2},\mathbb{Z}_{p}[Q],\unicode[STIX]{x1D706}_{0}^{i})$ with 
$i\in Z_{p}\cup \{p-1\}$, 
$|\text{cap}_{0}^{1}|=1$, 
$|\text{cap}_{0}^{2}|=p$ and 
$|\text{cap}_{1}^{2}|=p^{i}$.
$\text{(iii)}~V=(R_{2},\mathbb{Z}_{p},1)\oplus R_{1}$, 
$|\text{cap}_{0}^{1}|=|\text{cap}_{0}^{2}|=p$ and 
$|\text{cap}_{1}^{2}|=p^{p-1}$.
$\text{(iv)}~V=R_{2}\oplus \mathbb{Z}_{p}[Q]$, 
$|\text{cap}_{0}^{1}|=1$, 
$|\text{cap}_{0}^{2}|=p$ and 
$|\text{cap}_{1}^{2}|=p^{p}$.
$\text{(v)}~~V=R_{2}\oplus R_{1}\oplus \mathbb{Z}_{p}$, 
$|\text{cap}_{0}^{1}|=p$, 
$\text{cap}_{0}^{2}\cong (\mathbb{Z}/p)^{2}$ and 
$|\text{cap}_{1}^{2}|=p^{p}$.
$\text{(vi)}~V=(R_{2},R_{1},1)$, 
$|\text{cap}_{0}^{1}|=p$, 
$\text{cap}_{0}^{2}\cong \mathbb{Z}/p^{2}$ and 
$|\text{cap}_{1}^{2}|=p$.
$\text{(vi)}_{i}~V=(R_{2},R_{1},\unicode[STIX]{x1D706}_{0}^{i})$ with 
$i\in Z_{p}$, 
$|\text{cap}_{0}^{1}|=p$, 
$\text{cap}_{0}^{2}\cong (\mathbb{Z}/p)^{2}$ and 
$|\text{cap}_{1}^{2}|=p^{i+1}$.
Proof. The given conditions on 
$k$ imply that it satisfies Hypothesis 4.5 and so (18) gives an isomorphism of the form 
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{2},\unicode[STIX]{x1D6F4}}^{\times }\cong \mathbb{Z}_{p}[G]\oplus V^{\ast }$ with 
$V=V_{k_{2}/k}^{\ast }$. For each 
$a\in \{0,1,2\}$ this decomposition implies that 
$\text{rk}(V^{J_{a}})=\text{rk}(\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{2-a},\unicode[STIX]{x1D6F4}}^{\times })-\text{rk}(\mathbb{Z}_{p}[G/J_{a}])=p^{2-a},$ where we write 
$J_{a}$ for the subgroup of 
$G$ of order 
$p^{a}$.
The stated list of possibilities for 
$V$ is then obtained by explicitly comparing these rank conditions and the cohomology computations in (19) with the basic properties of the set of isomorphism classes of indecomposable 
$\mathbb{Z}_{p}[G]$-lattices, as recorded in [Reference Rzedowski-Calderón, Villa Salvador and Madan18, Table 2]. Since this process is entirely routine we leave all further details to the reader.◻
(i) Inspection of the list in Corollary 4.9 leads to several concrete observations about both Galois structures and capitulation kernels (under the given hypotheses). For example, the list combines with (18) to imply
$\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{2},\unicode[STIX]{x1D6F4}}^{\times }$ decomposes, in all cases, as a direct sum of ideals of $\mathbb{Z}_{p}[G]$ (whilst the Heller–Reiner classification implies that this is not true of every $\mathbb{Z}_{p}[G]$-lattice). It also implies that (as occurs, for example, whenever the class number of$$\begin{eqnarray}\displaystyle \text{cap}_{0}^{2}=0\Longleftrightarrow \text{cap}_{1}^{2}=0\Longleftrightarrow V\cong \mathbb{Z}_{p}[G] & & \displaystyle \nonumber\end{eqnarray}$$$k$ is prime to $p$), that or$$\begin{eqnarray}\displaystyle \text{cap}_{0}^{1}=0\Longleftrightarrow V\cong \mathbb{Z}_{p}[G] & & \displaystyle \nonumber\end{eqnarray}$$or$$\begin{eqnarray}\displaystyle V\cong R_{2}\oplus \mathbb{Z}_{p}[Q] & & \displaystyle \nonumber\end{eqnarray}$$for some$$\begin{eqnarray}\displaystyle V\cong (R_{2},\mathbb{Z}_{p}[Q],\unicode[STIX]{x1D706}_{0}^{i}) & & \displaystyle \nonumber\end{eqnarray}$$$i$ in $Z_{p}$, that and that in all cases one has$$\begin{eqnarray}\displaystyle \text{cap}_{0}^{2}~\text{has an element of order}~p^{2} & \Longleftrightarrow & \displaystyle |\text{cap}_{1}^{2}|\leqslant |\text{cap}_{0}^{1}|\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle V\cong (R_{2},R_{1},1)\nonumber\end{eqnarray}$$$|\text{cap}_{0}^{2}|\leqslant p\cdot |\text{cap}_{0}^{1}|$.(ii) Corollary 4.9 shows, in addition, that the structure of the
$\mathbb{Z}_{p}[G]$-module $\mathbb{Z}_{p}\otimes _{\mathbb{Z}}{\mathcal{O}}_{k_{2},\unicode[STIX]{x1D6F4}}^{\times }$ is completely determined by the abstract structures of the groups $\text{cap}_{k_{a},p}^{k_{2}}$ and $\text{cap}_{k,p}^{k_{1}}$. In particular, contrary to the more general result of Theorem 4.3, in this case one does not require any information about maps between these groups.
Acknowledgments
It is a pleasure to thank Daniel Macias Castillo and Christian Wuthrich for helpful discussions and to thank the referees for several helpful suggestions.
