Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shirai, Susumu
1978.
A remark concerning the 2-adic number field.
Nagoya Mathematical Journal,
Vol. 71,
Issue. ,
p.
87.
Shirai, Susumu
1979.
On the central ideal class group of cyclotomic fields.
Nagoya Mathematical Journal,
Vol. 75,
Issue. ,
p.
133.
Shirai, Susumu
1979.
On Galois groups of class two extensions over the rational number field.
Nagoya Mathematical Journal,
Vol. 75,
Issue. ,
p.
121.
Furuta, Yoshiomi
1980.
A prime decomposition symbol for a non-abelian central extension which is abelian over a bicyclic biquadratic field.
Nagoya Mathematical Journal,
Vol. 79,
Issue. ,
p.
79.
Miyake, Katsuya
1983.
Central extensions and Schur’s multiplicators of Galois groups.
Nagoya Mathematical Journal,
Vol. 90,
Issue. ,
p.
137.
Opolka, Hans
1983.
Extensions of number fields defined by cohomology groups.
Nagoya Mathematical Journal,
Vol. 92,
Issue. ,
p.
179.
Heider, Franz-Peter
1984.
Kapitulationsproblem und knotentheorie.
Manuscripta Mathematica,
Vol. 46,
Issue. 1-3,
p.
229.
Miyake, Katsuya
1984.
On central extensions of a Galois extension of algebraic number fields.
Nagoya Mathematical Journal,
Vol. 93,
Issue. ,
p.
133.
Kuz'min, L. V.
1987.
Algebraic number fields.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 3,
p.
1930.
TAKEUCHI, Teruo
1994.
The Hasse norm principle modulo <i>m</i> of finite Galois extensions of algebraic number fields and a generalization of a theorem of Fröhlich on the <i>e</i>-divisibility of the class numbers of <i>e</i>-abelian fields.
Japanese journal of mathematics. New series,
Vol. 20,
Issue. 2,
p.
231.
Yamashita, Hiroshi
1999.
On the rank of the first radical layer of ap-class group of an algebraic number field.
Nagoya Mathematical Journal,
Vol. 156,
Issue. ,
p.
85.
Opolka, Hans
2001.
Lifting Problems in Group Cohomology and Applications.
Journal of Mathematical Sciences,
Vol. 106,
Issue. 4,
p.
3222.

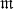 of Galois extensions of an algebraic number field
of Galois extensions of an algebraic number field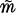 whose degree is some power of a prime
whose degree is some power of a prime 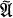 be the module of
be the module of 