No CrossRef data available.
Article contents
On Some Doubly Transitive Permutation Groups of Degree N And Order 6n(n – 1)
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let Ω be the set of symbols 1,2,..., n. Let 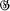 be a doubly transitive group on Ω of order 6n(n — 1) not containing a regular normal subgroup and let
be a doubly transitive group on Ω of order 6n(n — 1) not containing a regular normal subgroup and let 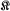 be the stabilizer of the set of symbols 1 and 2.
be the stabilizer of the set of symbols 1 and 2.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1970
References
[1]
Feit, W., On a class of doubly transitive permutation groups, 111. J. Math., 4 (1960), 170–186.Google Scholar
[2]
Gorenstein, D. and Walter, J.H., The characterization of finite groups with dihedral Sylow 2-subgroups, I, II, III, J. Alg., 2 (1965), 85–151, 218–270, 334–393.Google Scholar
[3]
Ito, N., On a class of doubly transitive permutation groups, 111. J. Math., 6 (1962), 341–352.Google Scholar
[4]
Ito, N., On doubly transitive groups of degree n and order 2(n—1)n
. Nagoya Math. J., 27 (1966), 409–417.CrossRefGoogle Scholar
[6]
Kimura, H., On doubly transitive permutation groups of degree n and order 4(n—l)n
, J. Math. Soc. Japan (to appear).Google Scholar
[7]
Kimura, H., On some doubly transitive permutation groups of degree n and order 2l(n—1)n
, (to appear).Google Scholar
[8]
Lüneburg, H., Charakterisierungen der endlichen desarguesschen Ebenen, Math. Z. 85 (1964), 419–450.CrossRefGoogle Scholar
[10]
Zassenhaus, H., Kennzeichnung endlicher linearer Gruppen als Permutationsgruppen, Hamb. Abh., 11 (1936), 17–40.Google Scholar

