No CrossRef data available.
Article contents
On singular sets of flat holomorphic mappings with isolated singularities
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In [4] B. Iversen studied critical points of algebraic mappings, using algebraic-geometry methods. In particular when algebraic maps have only isolated singularities, he shows the following relation; Let V and S be compact connected non-singular algebraic varieties of dimcV = n, and dimc S = 1, respectively. Suppose f is an algebraic map of V onto S with isolated singularities. Then it follows that
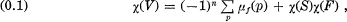
where χ denotes the Euler number, μf (p) is the Milnor number of f at the singular point p, and F is the general fiber of f : V → S.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1978
References
[1]
Borel, A. and Hirzebruch, F., Characteristic classes and homogeneous spaces I, Amer. J. Math. 80 (1958), 458–538.Google Scholar
[2]
Bott, R. and Chern, S. S., Hermitian vector bundles and equidistribution of the zeros of their holomorphic sections, Acta Math. 114 (1965), 71–112.CrossRefGoogle Scholar
[3]
Gunning, R. C. and Rossi, H., Analytic functions of several complex variables, Prentice-Hall, New Jersey, 1965.Google Scholar
[4]
Iversen, B., Critical points of an algebraic function, Inv. Math. 18 (1971), 210–224.CrossRefGoogle Scholar
[5]
Martinet, J., Sur les singularites des formes differentielles, Ann. Inst. Fourier, Grenoble
20 (1970), 95–178.Google Scholar
[6]
Omoto, H., An integral formula for the Chern form of a hermitian bundles, Nagoya Math. J. 42 (1971), 135–172.CrossRefGoogle Scholar

