Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nakayama, Tadasi
1951.
A Remark on Finitely Generated Modules.
Nagoya Mathematical Journal,
Vol. 3,
Issue. ,
p.
139.
Curtis, Charles W.
1953.
Noncommutative extensions of Hilbert rings.
Proceedings of the American Mathematical Society,
Vol. 4,
Issue. 6,
p.
945.
Nagata, Masayoshi
1953.
On the Theory of Henselian Rings.
Nagoya Mathematical Journal,
Vol. 5,
Issue. ,
p.
45.
Rosenberg, Alex
and
Zelinsky, Daniel
1960.
On Amitsur’s complex.
Transactions of the American Mathematical Society,
Vol. 97,
Issue. 2,
p.
327.
Auslander, Maurice
and
Goldman, Oscar
1960.
The Brauer group of a commutative ring.
Transactions of the American Mathematical Society,
Vol. 97,
Issue. 3,
p.
367.
Pareigis, Bodo
1964.
�ber normale, zentrale, separable Algebren und Amitsur-Kohomologie.
Mathematische Annalen,
Vol. 154,
Issue. 4,
p.
330.
Ingraham, Edward C.
1966.
Inertial subalgebras of algebras over commutative rings.
Transactions of the American Mathematical Society,
Vol. 124,
Issue. 1,
p.
77.
Greco, Silvio
1968.
Algebras over nonlocal Hensel rings.
Journal of Algebra,
Vol. 8,
Issue. 1,
p.
45.
Burgess, W.D.
1969.
On Semi-Perfect Group Rings.
Canadian Mathematical Bulletin,
Vol. 12,
Issue. 5,
p.
645.
Ingraham, Edward C.
1969.
On the occasional equality of the lower and Jacobson radicals in noetherian rings.
Archiv der Mathematik,
Vol. 20,
Issue. 3,
p.
267.
Greco, Silvio
1969.
Algebras over nonlocal Hensel rings. II.
Journal of Algebra,
Vol. 13,
Issue. 1,
p.
48.
Brown, W. C.
and
Ingraham, E. C.
1970.
A characterization of semilocal inertial coefficient rings.
Proceedings of the American Mathematical Society,
Vol. 26,
Issue. 1,
p.
10.
Ingraham, E.C
1970.
Inertial subalgebras of complete algebras.
Journal of Algebra,
Vol. 15,
Issue. 1,
p.
1.
Valabrega, Paolo
1971.
Anelli Henseliani topologici - II.
Annali di Matematica Pura ed Applicata,
Vol. 91,
Issue. 1,
p.
305.
Valabrega, Paolo
1971.
Anelli Henseliani topologici.
Annali di Matematica Pura ed Applicata,
Vol. 91,
Issue. 1,
p.
283.
Wehlen, Joseph A.
1971.
Algebras of Finite Cohomological Dimension.
Nagoya Mathematical Journal,
Vol. 43,
Issue. ,
p.
127.
Azumaya, Goro
1972.
Ring Theory.
p.
9.
Gordon, Robert
and
Small, L.W
1972.
Piecewise domains.
Journal of Algebra,
Vol. 23,
Issue. 3,
p.
553.
Wehlen, Joseph A.
1973.
Triangular matrix algebras over Hensel rings.
Proceedings of the American Mathematical Society,
Vol. 37,
Issue. 1,
p.
69.
Miyashita, Yôichi
1973.
An Exact Sequence Associated with a Generalized Crossed Product.
Nagoya Mathematical Journal,
Vol. 49,
Issue. ,
p.
21.

 where
where 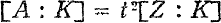 i.e. if the rank
i.e. if the rank 