Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shirosaki, Manabu
1993.
An extension of unicity theorem for meromorphic functions.
Tohoku Mathematical Journal,
Vol. 45,
Issue. 4,
Thoan, Pham Duc
Nam, Nguyen Hai
and
An, Nguyen Van
2019.
Second main theorems with weighted counting functions and its applications.
Indian Journal of Pure and Applied Mathematics,
Vol. 50,
Issue. 4,
p.
849.

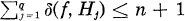 gives the best-possible estimate, where
gives the best-possible estimate, where 