Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bui, The Anh
and
Duong, Xuan Thinh
2021.
Spectral Multipliers of Self-Adjoint Operators on Besov and Triebel–Lizorkin Spaces Associated to Operators.
International Mathematics Research Notices,
Vol. 2021,
Issue. 23,
p.
18181.
Bui, The Anh
Duong, Xuan Thinh
Hong, Qing
and
Hu, Guorong
2023.
On Schrödinger Groups of Fractional Powers of Hermite Operators.
International Mathematics Research Notices,
Vol. 2023,
Issue. 7,
p.
6164.

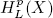 for 0
for 0 