Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ishikawa, Hideaki
2001.
Analytic Extension Formulas and their Applications.
Vol. 9,
Issue. ,
p.
105.
Akiyama, Shigeki
and
Tanigawa, Yoshio
2001.
Multiple Zeta Values at Non-Positive Integers.
The Ramanujan Journal,
Vol. 5,
Issue. 4,
p.
327.
Akiyama, Shigeki
and
Ishikawa, Hideaki
2002.
Analytic Number Theory.
Vol. 6,
Issue. ,
p.
1.
Matsumoto, Kohji
2003.
The analytic continuation and the asymptotic behaviour of certain multiple zeta-functions I.
Journal of Number Theory,
Vol. 101,
Issue. 2,
p.
223.
Matsumoto, Kohji
and
Tanigawa, Yoshio
2003.
The analytic continuation and the order estimate of multiple Dirichlet series.
Journal de théorie des nombres de Bordeaux,
Vol. 15,
Issue. 1,
p.
267.
Matsumoto, Kohji
2003.
Asymptotic expansions of double zeta-functions of Barnes, of Shintani, and Eisenstein series.
Nagoya Mathematical Journal,
Vol. 172,
Issue. ,
p.
59.
Ohno, Yasuo
2005.
Zeta Functions, Topology and Quantum Physics.
Vol. 14,
Issue. ,
p.
131.
Dienstfrey, Andrew
and
Huang, Jingfang
2006.
Integral representations for elliptic functions.
Journal of Mathematical Analysis and Applications,
Vol. 316,
Issue. 1,
p.
142.
Kamano, Ken
2006.
The Multiple Hurwitz Zeta Function and a Generalization of Lerch's Formula.
Tokyo Journal of Mathematics,
Vol. 29,
Issue. 1,
Matsumoto, Kohji
2006.
Number Theory.
Vol. 15,
Issue. ,
p.
153.
Guo, Li
and
Zhang, Bin
2008.
Renormalization of multiple zeta values.
Journal of Algebra,
Vol. 319,
Issue. 9,
p.
3770.
Guo, Li
and
Zhang, Bin
2008.
Differential Algebraic Birkhoff Decomposition and the renormalization of multiple zeta values.
Journal of Number Theory,
Vol. 128,
Issue. 8,
p.
2318.
DE CRISENOY, Marc
and
ESSOUABRI, Driss
2008.
Relations between values at T -tuples of negative integers of twisted multivariable zeta series associated to polynomials of several variables.
Journal of the Mathematical Society of Japan,
Vol. 60,
Issue. 1,
Zlobin, S. A.
2008.
Relations for multiple zeta values.
Mathematical Notes,
Vol. 84,
Issue. 5-6,
p.
771.
YAMAZAKI, Chika
2009.
ON THE DUALITY FOR MULTIPLE ZETA-STAR VALUES OF HEIGHT ONE.
Kyushu Journal of Mathematics,
Vol. 64,
Issue. 1,
p.
145.
Coppo, Marc-Antoine
and
Candelpergher, Bernard
2010.
The Arakawa–Kaneko zeta function.
The Ramanujan Journal,
Vol. 22,
Issue. 2,
p.
153.
Bayad, Abdelmejid
and
Hamahata, Yoshinori
2011.
Arakawa–Kaneko L-functions and generalized poly-Bernoulli polynomials.
Journal of Number Theory,
Vol. 131,
Issue. 6,
p.
1020.
Aoki, Takashi
Ohno, Yasuo
and
Wakabayashi, Noriko
2011.
On generating functions of multiple zeta values and generalized hypergeometric functions.
Manuscripta Mathematica,
Vol. 134,
Issue. 1-2,
p.
139.
BAYAD, Abdelmejid
and
HAMAHATA, Yoshinori
2011.
POLYLOGARITHMS AND POLY-BERNOULLI POLYNOMIALS.
Kyushu Journal of Mathematics,
Vol. 65,
Issue. 1,
p.
15.
Komori, Yasushi
Matsumoto, Kohji
and
Tsumura, Hirofumi
2011.
Shuffle products for multiple zeta values and partial fraction decompositions of zeta-functions of root systems.
Mathematische Zeitschrift,
Vol. 268,
Issue. 3-4,
p.
993.

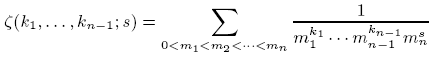 and show that the poly-Bernoulli numbers introduced in our previous paper are expressed as special values at negative arguments of certain combinations of these functions. As a consequence of our study, we obtain a series of relations among multiple zeta values.
and show that the poly-Bernoulli numbers introduced in our previous paper are expressed as special values at negative arguments of certain combinations of these functions. As a consequence of our study, we obtain a series of relations among multiple zeta values.