Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
KAWAMOTO, Fuminori
and
TOMITA, Koshi
2012.
Continued Fractions and Gauss' Class Number Problem for Real Quadratic Fields.
Tokyo Journal of Mathematics,
Vol. 35,
Issue. 1,
Özer, Ö.
2016.
A note on the fundamental unit in some types of the real quadratic number fields.
Vol. 1773,
Issue. ,
p.
050004.
Lee, Jungyun
and
Lee, Yoonjin
2017.
Regulators of an Infinite Family of the
Simplest Quartic Function Fields.
Canadian Journal of Mathematics,
Vol. 69,
Issue. 3,
p.
579.
Özer, Özen
and
Salem, Abdel Badeh M.
2017.
A computational technique for determining the fundamental unit in explicit types of real quadratic number fields.
International Journal of ADVANCED AND APPLIED SCIENCES,
Vol. 4,
Issue. 2,
p.
22.
Özer, Özen
2020.
A Handy Technique for Fundamental Unit in Specific Type of Real Quadratic Fields.
Applied Mathematics and Nonlinear Sciences,
Vol. 5,
Issue. 1,
p.
495.
Özer, Özen
2020.
Fundamental units for real quadratic fields determined by continued fraction conditions.
AIMS Mathematics,
Vol. 5,
Issue. 4,
p.
2899.

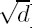 ]. Let
]. Let 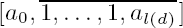 .
.