Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Deheuvels, Paul
and
Lifshits, Mikhail A.
1993.
Strassen-type functional laws for strong topologies.
Probability Theory and Related Fields,
Vol. 97,
Issue. 1-2,
p.
151.
Atlagh, Mohamed
and
Weber, Michel
1996.
Convergence in Ergodic Theory and Probability.
p.
41.
Schneider, Dominique
and
Weber, Michel
1996.
Convergence in Ergodic Theory and Probability.
p.
397.
Deheuvels, Paul
1997.
Strong laws for local quantile processes.
The Annals of Probability,
Vol. 25,
Issue. 4,
Lifshits, M. A.
and
Weber, M.
1997.
Strassen Laws of Iterated Logarithm for Partially Observed Processes.
Journal of Theoretical Probability,
Vol. 10,
Issue. 1,
p.
101.
Deheuvels, Paul
2000.
Nonstandard strong laws for local quantile processes.
Journal of Statistical Planning and Inference,
Vol. 91,
Issue. 2,
p.
239.
Gorn, N. L.
and
Lifshits, M. A.
2000.
On the functional law of the iterated logarithm for partially observed sums of random variables.
Journal of Mathematical Sciences,
Vol. 99,
Issue. 2,
p.
1061.
Dindar, Zacharie
2000.
Some results on increments of the partially observed empirical process.
Transactions of the American Mathematical Society,
Vol. 353,
Issue. 2,
p.
427.
Dindar, Zacharie
2003.
Some more results on increments of the partially observed empirical process.
Statistics & Probability Letters,
Vol. 64,
Issue. 1,
p.
25.
Weber, Mihel
2004.
Some examples of application of the metric entropy method.
Acta Mathematica Hungarica,
Vol. 105,
Issue. 1-2,
p.
39.
Berkes, István
and
Weber, Michel
2005.
Upper–lower class tests and frequency results along subsequences.
Stochastic Processes and their Applications,
Vol. 115,
Issue. 4,
p.
679.
Fukuyama, K.
and
Takeuchi, Y.
2008.
The law of the iterated logarithm for subsequences: A simple proof.
Lobachevskii Journal of Mathematics,
Vol. 29,
Issue. 3,
p.
130.
Weber, M.
2010.
A remark on the LIL for subsequences.
Lobachevskii Journal of Mathematics,
Vol. 31,
Issue. 4,
p.
336.
Weber, Michel J. G.
2024.
Critical probabilistic characteristics of the Cramér model for primes and arithmetical properties.
Indian Journal of Pure and Applied Mathematics,

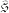 be any increasing sequence of integers and
be any increasing sequence of integers and 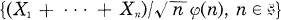 almost surely coincides with the unit ball of
almost surely coincides with the unit ball of 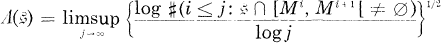 .
.