Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-26T20:29:03.508Z Has data issue: false hasContentIssue false
  • English
  • Français

LAURICELLA HYPERGEOMETRIC FUNCTIONS, UNIPOTENT FUNDAMENTAL GROUPS OF THE PUNCTURED RIEMANN SPHERE, AND THEIR MOTIVIC COACTIONS

Part of: Cycles and subschemes (Co)homology theory

Published online by Cambridge University Press:  26 September 2022

FRANCIS BROWN Open the ORCID record for FRANCIS BROWN [Opens in a new window]  and
CLÉMENT DUPONT Open the ORCID record for CLÉMENT DUPONT [Opens in a new window]
FRANCIS BROWN
Affiliation:
All Souls College University of Oxford Oxford OX1 4AL United Kingdom francis.brown@all-souls.ox.ac.uk
CLÉMENT DUPONT
Affiliation:
Institut Montpelliérain Alexander Grothendieck Université de Montpellier CNRS Montpellier France clement.dupont@umontpellier.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The goal of this paper is to raise the possibility that there exists a meaningful theory of ‘motives’ associated with certain hypergeometric integrals, viewed as functions of their parameters. It goes beyond the classical theory of motives, but should be compatible with it. Such a theory would explain a recent and surprising conjecture arising in the context of scattering amplitudes for a motivic Galois group action on Gauss’s 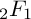${}_2F_1$ hypergeometric function, which we prove in this paper by direct means. More generally, we consider Lauricella hypergeometric functions and show, on the one hand, how the coefficients in their Taylor expansions can be promoted, via the theory of motivic fundamental groups, to motivic multiple polylogarithms. The latter are periods of ordinary motives and admit an action of the usual motivic Galois group, which we call the local action. On the other hand, we define lifts of the full Lauricella functions as matrix coefficients in a Tannakian category of twisted cohomology, which inherit an action of the corresponding Tannaka group. We call this the global action. We prove that these two actions, local and global, are compatible with each other, even though they are defined in completely different ways. The main technical tool is to prove that metabelian quotients of generalised Drinfeld associators on the punctured Riemann sphere are hypergeometric functions. We also study single-valued versions of these hypergeometric functions, which may be of independent interest.

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives
Secondary: 14F35: Homotopy theory; fundamental groups 33C05: Classical hypergeometric functions, $_2F_1$ 33C70: Other hypergeometric functions and integrals in several variables
Type
Article
Information
Nagoya Mathematical Journal , Volume 249 , March 2023 , pp. 148 - 220
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 724638). Clément Dupont was partially supported by the grant PERGAMO from the Agence Nationale de la Recherche (ANR-18-CE40-0017).

References

Abreu, S., Britto, R., Duhr, C., and Gardi, E., Algebraic structure of cut Feynman integrals and the diagrammatic coaction , Phys. Rev. Lett. 119 (2017), no. 5, 051601.CrossRefGoogle ScholarPubMed
Abreu, S., Britto, R., Duhr, C., and Gardi, E., Diagrammatic Hopf algebra of cut Feynman integrals: The one-loop case , J. High Energy Phys. 2017, 90.CrossRefGoogle Scholar
Abreu, S., Britto, R., Duhr, C., Gardi, E., and Matthew, J., “Diagrammatic coaction of two-loop Feynman integrals” in Proceedings of Science 14th International Symposium on Radiative Corrections, Trieste, Italy, 2019.Google Scholar
Abreu, S., Britto, R., Duhr, C., Gardi, E., and Matthew, J., From positive geometries to a coaction on hypergeometric functions , J. High Energy Phys. 2020, 1–45.Google Scholar
Aomoto, K., On vanishing of cohomology attached to certain many valued meromorphic functions , J. Math. Soc. Japan 27 (1975), 248–255.CrossRefGoogle Scholar
Aomoto, K., On the complex Selberg integral , Q. J. Math. 38 (1987), 385–399.CrossRefGoogle Scholar
Belavin, A. A., Polyakov, A. M., and Zamolodchikov, A. B., Infinite conformal symmetry in two-dimensional quantum field theory , Nucl. Phys. 241 (1984), 333–380.CrossRefGoogle Scholar
Broedel, J., Schlotterer, O., Stieberger, S., and Terasoma, T., All order ${\alpha}^{\prime }$ -expansion of superstring trees from the Drinfeld associator , Phys. Rev. D 89 (2014), 066014.CrossRefGoogle Scholar
Brown, F., “Motivic periods and  $\mathbb{P}^{1}\backslash \{0,1,\infty\}$ ” in Proceedings of the International Congress of Mathematicians – Seoul 2014, II, Kyung Moon Sa, Seoul, 2014, 295–318.Google Scholar
Brown, F., Single-valued motivic periods and multiple zeta values , Forum Math. Sigma 2 (2014), art. ID e25.CrossRefGoogle Scholar
Brown, F., Notes on motivic periods , Commun. Number Theory Phys. 11 (2017), 557–655.CrossRefGoogle Scholar
Brown, F. and Dupont, C., Single-valued integration and double copy , J. Reine Angew. Math. 775 (2021), 145–196.CrossRefGoogle Scholar
Brown, F. and Dupont, C., Single-valued integration and superstring amplitudes in genus zero , Commun. Math. Phys. 382 (2021), 815–874.CrossRefGoogle ScholarPubMed
Burgos Gil, J. I. and Fresán, J., Multiple zeta values: From numbers to motives, to appear in Clay Mathematics Proceedings (2017).Google Scholar
Cho, K. and Matsumoto, K., Intersection theory for twisted cohomologies and twisted Riemann’s period relations I , Nagoya Math. J. 139 (1995), 67–86.CrossRefGoogle Scholar
Deligne, P., Équations Différentielles à Points Singuliers Réguliers, Lecture Notes in Math. 163, Springer, Berlin–New York, 1970.CrossRefGoogle Scholar
Deligne, P. and Goncharov, A. B., Groupes fondamentaux motiviques de Tate mixte , Ann. Sci. École Norm. Sup. (4) 38 (2005), 1–56.CrossRefGoogle Scholar
Deligne, P. and Mostow, G. D., Monodromy of hypergeometric functions and nonlattice integral monodromy , Inst. Hautes Études Sci. Publ. Math. 63 (1986), 5–89.CrossRefGoogle Scholar
Dotsenko, V. S. and Fateev, V. A., Four-point correlation functions and the operator algebra in $2$ D conformal invariant theories with central charge $C\le 1$ , Nucl. Phys. 251 (1985), 691–734.CrossRefGoogle Scholar
Drinfeld, V. G., On quasitriangular quasi-Hopf algebras and on a group that is closely connected with $Gal\left(\overline{\mathbb{Q}}/ \mathbb{Q}\right)$ , Algebra i Analiz 2 (1990), 149–181.Google Scholar
Enriquez, B., On the Drinfeld generators of ${grt}_1(k)$ and $\varGamma$ -functions for associators , Math. Res. Lett. 13 (2006), 231–243.CrossRefGoogle Scholar
Esnault, H. and Levine, M., Tate motives and the fundamental group, preprint, arXiv:0708.4034 Google Scholar
Esnault, H., Schechtman, V., and Viehweg, E., Cohomology of local systems on the complement of hyperplanes , Invent. Math. 109 (1992), 557–561.CrossRefGoogle Scholar
Goto, Y., Twisted period relations for Lauricella’s hypergeometric functions ${F}_A$ , Osaka J. Math. 52 (2015), 861–879.Google Scholar
Hanamura, M. and Yoshida, M., Hodge structure on twisted cohomologies and twisted Riemann inequalities I , Nagoya Math. J. 154 (1999), 123–139.CrossRefGoogle Scholar
Hattori, A. and Kimura, T., On the Euler integral representations of hypergeometric functions in several variables , J. Math. Soc. Japan 26 (1974), 1–16.CrossRefGoogle Scholar
Ihara, Y., Kaneko, M., and Yukinari, A., “On some properties of the universal power series for Jacobi sums” in Galois Representations and Arithmetic Algebraic Geometry (Kyoto, 1985/Tokyo, 1986), Adv. Stud. Pure Math. 12, North-Holland, Amsterdam, 1987, 65–86.Google Scholar
Kawai, H., Lewellen, D. C., and Tye, S.-H. H., A relation between tree amplitudes of closed and open strings , Nucl. Phys. B 269 (1986), 1–23.CrossRefGoogle Scholar
Kita, M. and Noumi, M., On the structure of cohomology groups attached to the integral of certain many-valued analytic functions , Jpn. J. Math. (N.S.) 9 (1983), 113–157.CrossRefGoogle Scholar
Kita, M. and Yoshida, M., Intersection theory for twisted cycles , Math. Nachr. 166 (1994), 287–304.CrossRefGoogle Scholar
Kita, M. and Yoshida, M., Intersection theory for twisted cycles II—Degenerate arrangements , Math. Nachr. 168 (1994), 171–190.CrossRefGoogle Scholar
Knizhnik, V. G. and Zamolodchikov, A. B., Current algebra and Wess–Zumino model in two dimensions , Nucl. Phys. 247 (1984), 83–103.CrossRefGoogle Scholar
Kontsevich, M. and Zagier, D., “Periods” in Mathematics Unlimited—2001 and Beyond, Springer, Berlin, 2001, 771–808.CrossRefGoogle Scholar
Li, Z., Gamma series associated to elements satisfying regularized double shuffle relations , J. Number Theory 130 (2010), 213–231.CrossRefGoogle Scholar
Loeser, F. and Sabbah, C., Equations aux différences finies et déterminants d’intégrales de fonctions multiformes , Comment. Math. Helv. 66 (1991), 458–503.CrossRefGoogle Scholar
Matsumoto, K., Intersection numbers for logarithmic $k$ -forms , Osaka J. Math. 35 (1998), 873–893.Google Scholar
Matthes, N., The meta-abelian elliptic KZB associator and periods of Eisenstein series , Sel. Math. New Ser. 24 (2018), 3217–3239.CrossRefGoogle Scholar
Mimachi, K., “Complex hypergeometric integrals” in Representation Theory, Special Functions and Painlevé Equations—RIMS 2015, Math. Soc. Kyoto, Japan, 2018, 469–485.CrossRefGoogle Scholar
Mimachi, K. and Yoshida, M., Intersection numbers of twisted cycles and the correlation functions of the conformal field theory , Commun. Math. Phys. 234 (2003), 339–358.CrossRefGoogle Scholar
Mizera, S., Combinatorics and topology of Kawai–Lewellen–Tye relations , J. High Energy Phys. 2017, 97.CrossRefGoogle Scholar
Nakamura, H., On exterior Galois representations associated with open elliptic curves , J. Math. Sci. Univ. Tokyo 2 (1995), 197–231.Google Scholar
Schlotterer, O. and Schnetz, O., Closed strings as single-valued open strings: A genus-zero derivation , J. Phys. A: Math. Theor. 52 (2019), 045401.CrossRefGoogle Scholar
Schlotterer, O. and Stieberger, S., Motivic multiple zeta values and superstring amplitudes , J. Phys. A: Math. Theor. 46 (2013), no. 47, 475401.CrossRefGoogle Scholar
Vanhove, P. and Zerbini, F., Closed string amplitudes from single-valued correlation functions, preprint, arXiv:1812.03018 Google Scholar