Article contents
GENERALIZED ZETA INTEGRALS ON CERTAIN REAL PREHOMOGENEOUS VECTOR SPACES
Published online by Cambridge University Press: 05 September 2022
Abstract
Let X be a real prehomogeneous vector space under a reductive group G, such that X is an absolutely spherical G-variety with affine open orbit. We define local zeta integrals that involve the integration of Schwartz–Bruhat functions on X against generalized matrix coefficients of admissible representations of 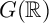 $G(\mathbb {R})$, twisted by complex powers of relative invariants. We establish the convergence of these integrals in some range, the meromorphic continuation, as well as a functional equation in terms of abstract
$G(\mathbb {R})$, twisted by complex powers of relative invariants. We establish the convergence of these integrals in some range, the meromorphic continuation, as well as a functional equation in terms of abstract 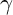 $\gamma $-factors. This subsumes the archimedean zeta integrals of Godement–Jacquet, those of Sato–Shintani (in the spherical case), and the previous works of Bopp–Rubenthaler. The proof of functional equations is based on Knop’s results on Capelli operators.
$\gamma $-factors. This subsumes the archimedean zeta integrals of Godement–Jacquet, those of Sato–Shintani (in the spherical case), and the previous works of Bopp–Rubenthaler. The proof of functional equations is based on Knop’s results on Capelli operators.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal
Footnotes
This work is supported by the National Natural Science Foundation of China (Grant No. 11922101).
References
- 1
- Cited by


