Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ma, Linquan
Schwede, Karl
and
Shimomoto, Kazuma
2017.
Local cohomology of Du Bois singularities and applications to families.
Compositio Mathematica,
Vol. 153,
Issue. 10,
p.
2147.
Puthenpurakal, Tony J.
and
Reddy, Rakesh B. T.
2018.
On a Relation Between de Rham Cohomology of H
(f)
1
(R) and the Koszul Cohomology of ∂(f) in R/(f).
Indian Journal of Pure and Applied Mathematics,
Vol. 49,
Issue. 1,
p.
71.
PUTHENPURAKAL, TONY J.
and
SINGH, JYOTI
2019.
On derived functors of graded local cohomology modules.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 167,
Issue. 3,
p.
549.
Puthenpurakal, Tony J.
Roy, Sudeshna
and
Singh, Jyoti
2020.
On derived functors of graded local cohomology modules—II.
Illinois Journal of Mathematics,
Vol. 64,
Issue. 4,
Walther, Uli
and
Zhang, Wenliang
2021.
Commutative Algebra.
p.
773.
Patle, Aarti
and
Singh, Jyoti
2021.
Generalized Eulerian 𝒟-modules in char p > 0.
Journal of Algebra and Its Applications,
Vol. 20,
Issue. 07,
p.
2150127.
Puthenpurakal, Tony J.
2022.
Graded components of local cohomology modules.
Collectanea Mathematica,
Vol. 73,
Issue. 1,
p.
135.
Puthenpurakal, Tony J.
and
Roy, Sudeshna
2024.
Graded Components of Local Cohomology Modules II.
Vietnam Journal of Mathematics,
Vol. 52,
Issue. 1,
p.
1.
Patle, Aarti
and
Singh, Jyoti
2025.
On the graded injective hull of R/𝔭 in prime characteristic.
Journal of Algebra and Its Applications,
Vol. 24,
Issue. 12,
Puthenpurakal, Tony J.
2025.
Graded Components of Local Cohomology Modules Over Invariant Rings-II.
Vietnam Journal of Mathematics,
Vol. 53,
Issue. 2,
p.
323.
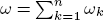 . Let I be a graded ideal in R. By a result due to Lyubeznik the local cohomology modules
. Let I be a graded ideal in R. By a result due to Lyubeznik the local cohomology modules 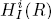 are holonomic (An (K))-modules for each i≥0. In this article we prove that the de Rham cohomology modules
are holonomic (An (K))-modules for each i≥0. In this article we prove that the de Rham cohomology modules 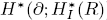 are concentrated in degree —ω; that is,
are concentrated in degree —ω; that is, 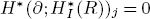 for j ≠ –ω. As an application when A = R/(f) is an isolated singularity, we relate
for j ≠ –ω. As an application when A = R/(f) is an isolated singularity, we relate 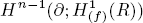 to Hn-1 (∂(f);A), the (n – 1)th Koszul cohomology of A with respect to ∂1 (f),…, ∂n (f).
to Hn-1 (∂(f);A), the (n – 1)th Koszul cohomology of A with respect to ∂1 (f),…, ∂n (f).