Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Faltings, Gerd
1980.
Ein Kriterium f�r vollst�ndige Durchschnitte.
Inventiones Mathematicae,
Vol. 62,
Issue. 3,
p.
393.
Rees, David
1989.
Commutative Algebra.
Vol. 15,
Issue. ,
p.
407.
Hochster, Melvin
and
Huneke, Craig
1991.
Absolute integral closures are big Cohen-Macaulay algebras in characteristic 𝑃.
Bulletin of the American Mathematical Society,
Vol. 24,
Issue. 1,
p.
137.
Bădescu, Lucian
1996.
Algebraic Barth-Lefschetz theorems.
Nagoya Mathematical Journal,
Vol. 142,
Issue. ,
p.
17.
Hübl, Reinhold
and
Swanson, Irena
2001.
Discrete valuations centered on local domains.
Journal of Pure and Applied Algebra,
Vol. 161,
Issue. 1-2,
p.
145.
Divaani-Aazar, K.
Naghipour, R.
and
Tousi, M.
2002.
THE LICHTENBAUM-HARTSHORNE THEOREM FOR GENERALIZED LOCAL COHOMOLOGY AND CONNECTEDNESS.
Communications in Algebra,
Vol. 30,
Issue. 8,
p.
3687.
Lyubeznik, Gennady
2007.
On some local cohomology modules.
Advances in Mathematics,
Vol. 213,
Issue. 2,
p.
621.
Bădescu, Lucian
and
Valla, Giuseppe
2010.
Grothendieck–Lefschetz theory, set-theoretic complete intersections and rational normal scrolls.
Journal of Algebra,
Vol. 324,
Issue. 7,
p.
1636.
Caravantes, Jorge
2012.
Bertini-type theorems for formal functions in Grassmannians.
Revista Matemática Complutense,
Vol. 25,
Issue. 1,
p.
157.
Bădescu, Lucian
2014.
Bridging Algebra, Geometry, and Topology.
Vol. 96,
Issue. ,
p.
85.
Caravantes, Jorge
and
Perrin, Nicolas
2014.
Formal properties in small codimension.
Collectanea Mathematica,
Vol. 65,
Issue. 2,
p.
251.
Hernández, Daniel J.
Núñez-Betancourt, Luis
Pérez, Felipe
and
Witt, Emily E.
2018.
Cohomological dimension, Lyubeznik numbers, and connectedness in mixed characteristic.
Journal of Algebra,
Vol. 514,
Issue. ,
p.
442.
Núñez-Betancourt, Luis
Spiroff, Sandra
and
Witt, Emily E
2019.
Connectedness and Lyubeznik Numbers.
International Mathematics Research Notices,
Vol. 2019,
Issue. 13,
p.
4233.

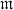 and if
and if 