Article contents
CONSTRUCTING NONPROXY SMALL TEST MODULES FOR THE COMPLETE INTERSECTION PROPERTY
Published online by Cambridge University Press: 21 June 2021
Abstract
A local ring R is regular if and only if every finitely generated R-module has finite projective dimension. Moreover, the residue field k is a test module: R is regular if and only if k has finite projective dimension. This characterization can be extended to the bounded derived category 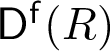 $\mathsf {D}^{\mathsf f}(R)$, which contains only small objects if and only if R is regular. Recent results of Pollitz, completing work initiated by Dwyer–Greenlees–Iyengar, yield an analogous characterization for complete intersections: R is a complete intersection if and only if every object in
$\mathsf {D}^{\mathsf f}(R)$, which contains only small objects if and only if R is regular. Recent results of Pollitz, completing work initiated by Dwyer–Greenlees–Iyengar, yield an analogous characterization for complete intersections: R is a complete intersection if and only if every object in 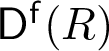 $\mathsf {D}^{\mathsf f}(R)$ is proxy small. In this paper, we study a return to the world of R-modules, and search for finitely generated R-modules that are not proxy small whenever R is not a complete intersection. We give an algorithm to construct such modules in certain settings, including over equipresented rings and Stanley–Reisner rings.
$\mathsf {D}^{\mathsf f}(R)$ is proxy small. In this paper, we study a return to the world of R-modules, and search for finitely generated R-modules that are not proxy small whenever R is not a complete intersection. We give an algorithm to construct such modules in certain settings, including over equipresented rings and Stanley–Reisner rings.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license
Footnotes
The second author was supported by the National Science Foundation grant DMS-2001445. The third author was supported by the National Science Foundation grant DMS-2002173 and the National Science Foundation Research Training Group grant DMS-1840190.
References
- 6
- Cited by


