Hostname: page-component-54dcc4c588-5q6g5 Total loading time: 0 Render date: 2025-09-21T06:43:22.963Z Has data issue: false hasContentIssue false
  • English
  • Français

A complex Airy integral

Published online by Cambridge University Press:  22 January 2016

Tomio Kubota
Tomio Kubota*
Affiliation:
Department of Mathematics, Nagoya University and Department of Mathematics, University of Maryland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Airy integral is a formula concerning the Fourier transform of a function like sin x3 or cos x3 , and is written, for instance in [2], as

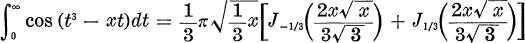
for x ≧ 0.

Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 61 , July 1976 , pp. 113 - 116
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1976

References

[1] Kubota, T., On a generalized Fourier transformation, to appear in J. Fac. Sci. Univ. Tokyo.Google Scholar
[2] Watson, G. N., A treatise on the theory of Bessel functions, Cambridge University Press, 1966.Google Scholar