Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-11T10:48:47.906Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPACT ORBITS OF PARABOLIC SUBGROUPS

Part of: Automorphic functions Complex spaces with a group of automorphisms

Published online by Cambridge University Press:  14 December 2021

LEONARDO BILIOTTI Open the ORCID record for LEONARDO BILIOTTI [Opens in a new window]  and
OLUWAGBENGA JOSHUA WINDARE Open the ORCID record for OLUWAGBENGA JOSHUA WINDARE [Opens in a new window]
LEONARDO BILIOTTI
Affiliation:
Dipartimento di Scienze Matematiche, Fisiche e Informatiche Università di Parma, Parma, Italy leonardo.biliotti@unipr.it
OLUWAGBENGA JOSHUA WINDARE
Affiliation:
Dipartimento di Scienze Matematiche, Fisiche e Informatiche Università di Parma, Parma, Italy oluwagbengajoshua.windare@unipr.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the action of a real reductive group G on a real submanifold X of a Kähler manifold Z. We suppose that the action of a compact connected Lie group U with Lie algebra 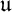$\mathfrak {u}$ extends holomorphically to an action of the complexified group 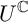$U^{\mathbb {C}}$ and that the U-action on Z is Hamiltonian. If 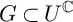$G\subset U^{\mathbb {C}}$ is compatible, there exists a gradient map 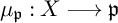$\mu _{\mathfrak p}:X \longrightarrow \mathfrak p$ where 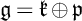$\mathfrak g=\mathfrak k \oplus \mathfrak p$ is a Cartan decomposition of 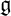$\mathfrak g$ . In this paper, we describe compact orbits of parabolic subgroups of G in terms of the gradient map $\mu _{\mathfrak p}$ .

MSC classification

Primary: 57S20: Noncompact Lie groups of transformations
Secondary: 32M05: Complex Lie groups, automorphism groups acting on complex spaces
Type
Article
Information
Nagoya Mathematical Journal , Volume 247 , September 2022 , pp. 615 - 623
Check for updates
Copyright
© (2021) The Authors. Copyright in the Journal, as distinct from the individual articles, is owned by Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Biliotti was partially supported by the Project PRIN 2015, Real and Complex Manifolds: Geometry, Topology and Harmonic Analysis, by the Project PRIN 2017, Real and Complex Manifolds: Topology, Geometry and Holomorphic Dynamics, and by the GNSAGA INdAM.

References

Akhiezer, D. N., Lie Group Actions in Complex Analysis, Asp. Math. E27, Friedr. Vieweg, Braunschweig, 1995.Google Scholar
Atiyah, M. F., Convexity and commuting Hamiltonians , Bull. Lond. Math. Soc. 14 (1982), 1–15.Google Scholar
Biliotti, L., Satake–Furstenberg compactifications and gradient map, preprint, arXiv:2012.14858 Google Scholar
Biliotti, L., Ghigi, A., and Heinzner, P., Coadjoint orbitopes , Osaka J. Math. 51 (2014), 935–968.Google Scholar
Biliotti, L., Ghigi, A., and Heinzner, P., Polar orbitopes , Comm. Ann. Geom. 21 (2013), 1–28.Google Scholar
Borel, A. and Ji, L., Compactifications of Symmetric and Locally Symmetric Spaces, Math. Theory Appl., Birkhäuser Boston, Boston, MA, 2006.Google Scholar
Guillemin, V. and Sternberg, S., Convexity properties of the moment mapping , Invent. Math. 67 (1982), 491–513.CrossRefGoogle Scholar
Guillemim, V. and Sternberg, S., Symplectic Techniques in Physics, 2nd ed., Cambridge Univ. Press, Cambridge, 1990.Google Scholar
Heinzner, P., Schwarz, G. W., and Stötzel, H., Stratifications with respect to actions of real reductive groups , Compos. Math. 144 (2008), 163–185.Google Scholar
Heinzner, P. and Stötzel, H., Semistable points with respect to real forms , Math. Ann. 338 (2007), 1–9.Google Scholar
Helgason, S., Differential Geometry, Lie Groups, and Symmetric Spaces, Pure Appl. Math. 80, Academic Press, New York, 1978.Google Scholar
Kirwan, F., Cohomology of Quotients in Symplectic and Algebraic Geometry, Math. Notes 31, Princeton Univ. Press, Princeton, NJ, 1984.Google Scholar
Knapp, A. W., Lie Groups Beyond an Introduction, 2nd ed., Progr. Math. 140, Birkhäuser Boston, Boston, MA, 2002.Google Scholar
Kostant, B., On convexity, the Weyl group and the Iwasawa decomposition , Ann. Sci. Éc. Norm. Supér. (4) 6 (1973), 413–455.CrossRefGoogle Scholar
Schneider, R., Convex Bodies: The Brunn–Minkowski Theory, Encyclopedia Math. Appl. 44, Cambridge Univ. Press, Cambridge, 1993.Google Scholar
Wolf, J., The action of real of a real semisimple group on a complex flag manifold. I: Orbit structure and holomorphic arc components . Bull. Amer. Math. Soc. 75 (1969), 1121–1237.CrossRefGoogle Scholar