Article contents
ON THE HEIGHT AND RELATIONAL COMPLEXITY OF A FINITE PERMUTATION GROUP
Published online by Cambridge University Press: 13 July 2021
Abstract
Let G be a permutation group on a set  $\Omega $ of size t. We say that
$\Omega $ of size t. We say that  $\Lambda \subseteq \Omega $ is an independent set if its pointwise stabilizer is not equal to the pointwise stabilizer of any proper subset of
$\Lambda \subseteq \Omega $ is an independent set if its pointwise stabilizer is not equal to the pointwise stabilizer of any proper subset of 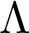 $\Lambda $. We define the height of G to be the maximum size of an independent set, and we denote this quantity
$\Lambda $. We define the height of G to be the maximum size of an independent set, and we denote this quantity 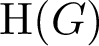 $\textrm{H}(G)$. In this paper, we study
$\textrm{H}(G)$. In this paper, we study  $\textrm{H}(G)$ for the case when G is primitive. Our main result asserts that either
$\textrm{H}(G)$ for the case when G is primitive. Our main result asserts that either 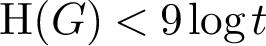 $\textrm{H}(G)< 9\log t$ or else G is in a particular well-studied family (the primitive large–base groups). An immediate corollary of this result is a characterization of primitive permutation groups with large relational complexity, the latter quantity being a statistic introduced by Cherlin in his study of the model theory of permutation groups. We also study
$\textrm{H}(G)< 9\log t$ or else G is in a particular well-studied family (the primitive large–base groups). An immediate corollary of this result is a characterization of primitive permutation groups with large relational complexity, the latter quantity being a statistic introduced by Cherlin in his study of the model theory of permutation groups. We also study 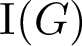 $\textrm{I}(G)$, the maximum length of an irredundant base of G, in which case we prove that if G is primitive, then either
$\textrm{I}(G)$, the maximum length of an irredundant base of G, in which case we prove that if G is primitive, then either  $\textrm{I}(G)<7\log t$ or else, again, G is in a particular family (which includes the primitive large–base groups as well as some others).
$\textrm{I}(G)<7\log t$ or else, again, G is in a particular family (which includes the primitive large–base groups as well as some others).
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license
Footnotes
Nick Gill and Pablo Spiga would like to acknowledge the support of the Engineering and Physical Sciences Research Council grant EP/R028702/1 over the course of this research.
References
- 11
- Cited by


