Hostname: page-component-857557d7f7-gtc7z Total loading time: 0.001 Render date: 2025-11-22T02:14:23.962Z Has data issue: false hasContentIssue false
  • English
  • Français

THE HYPERELLIPTIC THETA MAP AND OSCULATING PROJECTIONS

Published online by Cambridge University Press:  04 December 2020

MICHELE BOLOGNESI Open the ORCID record for MICHELE BOLOGNESI [Opens in a new window]  and
N. F. VARGAS
MICHELE BOLOGNESI*
Affiliation:
Institut Montpellierain Alexander Grothendieck Université de Montpellier CNRS Case Courrier 051 - Place Eugène Bataillon 34095 Montpellier Cedex 5 France
N. F. VARGAS
Affiliation:
Université de Rennes I CNRS IRMAR - UMR 6625 F-35000 Rennes France nestor.fernandez-vargas@univ-rennes1.fr
*
michele.bolognesi@umontpellier.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let C be a hyperelliptic curve of genus 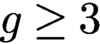$g \geq 3$. In this paper, we give a new geometric description of the theta map for moduli spaces of rank 2 semistable vector bundles on C with trivial determinant. In order to do this, we describe a fibration of (a birational model of) the moduli space, whose fibers are GIT quotients 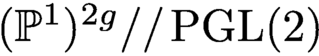$(\mathbb {P}^1)^{2g}//\text {PGL(2)}$. Then, we identify the restriction of the theta map to these GIT quotients with some explicit degree 2 osculating projection. As a corollary of this construction, we obtain a birational inclusion of a fibration in Kummer 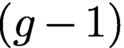$(g-1)$-varieties over 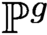$\mathbb {P}^g$ inside the ramification locus of the theta map.

Information

Type
Article
Information
Nagoya Mathematical Journal , Volume 245 , March 2022 , pp. 206 - 228
Check for updates
Copyright
© 2020 The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

*

Michele Bolognesi is member of the research groups GAGC and GNSAGA, whose support is acknowledged.

References

Alzati, A. and Bolognesi, M., A structure theorem for ${\mathbf{\mathcal{SU}}}_C(2)$ and the moduli of pointed rational curves , J. Algebraic Geom. 24 (2015), no. 2, 283–310.CrossRefGoogle Scholar
Arbarello, E., Cornalba, M., Griffiths, P. A., and Harris, J., Geometry of Algebraic Curves . Number vol. 1 in Grundlehren der mathematischen Wissenschaften, Springer-Verlag, New York, NY, 1985.CrossRefGoogle Scholar
Beauville, A., Narasimhan, M. S., and Ramanan, S., Spectral curves and the generalised theta divisor , J. Reine Angew. Math. 398 (1989), 169–179.Google Scholar
Bertram, A., Moduli of rank- $2$ vector bundles, theta divisors, and the geometry of curves in projective space , J. Differ. Geom. 35 (1992), no. 2, 429–469.CrossRefGoogle Scholar
Bolognesi, M., On Weddle surfaces and their moduli , Adv. Geom. 7 (2007), no. 1, 113–144.CrossRefGoogle Scholar
Bolognesi, M., A Conic Bundle Degenerating on the Kummer Surface , Math. Z. 261 (2009), no. 1, 149–168.CrossRefGoogle Scholar
Bolognesi, M., Forgetful linear systems on the projective space and rational normal curves over ${\mathbf{\mathcal{M}}}_{0,2n}^{GIT}$ , Bull. Lond. Math. Soc. 43 (2011), no. 3, 583–596.10.1112/blms/bdq125CrossRefGoogle Scholar
Bolognesi, M. and Brivio, S., Coherent systems and modular subvarieties of ${\mathbf{\mathcal{SU}}}_C(r)$ , Int. J. Math. 23 (2012), no. 4, 1250037.CrossRefGoogle Scholar
Brivio, S. and Verra, A., The theta divisor of ${\mathbf{\mathcal{SU}}}_C{\left(2,2d\right)}^s$ is very ample if $C$ is not hyperelliptic, Duke Math. J. 82 (1996), no. 3, 503–552.CrossRefGoogle Scholar
Brivio, S. and Verra, A., Plücker forms and the theta map , Amer. J. Math. 134 (2012), no. 5, 1247–1273.10.1353/ajm.2012.0034CrossRefGoogle Scholar
Desale, U. V. and Ramanan, S., Classification of vector bundles of rank $2$ on hyperelliptic curves , Invent. Math. 38 (1976/77), no. 2, 161–185.CrossRefGoogle Scholar
Dolgachev, I. and Ortland, D., Point sets in projective spaces and theta functions , Astérisque 165 (1988/89), 210 pp.Google Scholar
Dolgachev, I., Lectures on Invariant Theory , volume 296 of London Mathematical Society Lecture Note Series, Cambridge University Press, Cambridge, 2003.CrossRefGoogle Scholar
Dolgachev, I., Corrado Segre and nodal cubic threefolds. In From Classical to Modern Algebraic Geometry, Trends Hist. Sci. Birkhäuser/Springer, Cham, 2016, 429–450.CrossRefGoogle Scholar
Drezet, J.-M. and Narasimhan, M. S., Groupe de Picard des variétés de modules de fibrés semi-stables sur les courbes algébriques , Invent. Math. 97 (1989), no. 1, 53–94.CrossRefGoogle Scholar
Hitching, G. H. and Hoff, M., Tangent cones to generalised theta divisors and generic injectivity of the theta map , Compos. Math. 153 (2017), no. 12, 2643–2657.10.1112/S0010437X17007539CrossRefGoogle Scholar
Kapranov, M. M., Chow quotients of Grassmannians. I. In I. M. Gel’fand Seminar, volume 16 of Adv. Soviet Math. Amer. Math. Soc., Providence, RI, 1993, 29–110.Google Scholar
Kapranov, M. M., Veronese curves and Grothendieck-Knudsen moduli space ${\overline{M}}_{0,n}$ , J. Algebraic Geom. 2 (1993), no. 2, 239–262.Google Scholar
Keel, S. and McKernan, J., Contractible extremal rays on ${\overline{M}}_{0,n}$ . In Handbook of Moduli. volume 25 of Adv. Lect. Math. (ALM) II, Int. Press, Somerville, MA, 2013, 115–130.Google Scholar
Knudsen, F. F., The projectivity of the moduli space of stable curves. II. The stacks ${M}_{g,n}$ , Math. Scand. 52 (1983), no. 2, 161–199.CrossRefGoogle Scholar
Kumar, C., Invariant vector bundles of rank 2 on hyperelliptic curves , Mich. Math. J. 47 (2000), no. 3, 575–584.CrossRefGoogle Scholar
Kumar, C., Linear systems and quotients of projective space , Bull. Lond. Math. Soc. 35 (2003), no. 2, 152–160.CrossRefGoogle Scholar
Lange, H. and Narasimhan, M. S., Maximal subbundles of rank two vector bundles on curves , Math. Ann. 266 (1983), no. 1, 55–72.CrossRefGoogle Scholar
Massarenti, A. and Rischter, R., Non-secant defectivity via osculating projections Annali della Scuola Normale Superiore di Pisa, Classe di Scienze, 2019, Vol. XIX, 1–34CrossRefGoogle Scholar
Narasimhan, M. S. and Ramanan, S., Moduli of vector bundles on a compact Riemann surface . Ann. Math. 89 (1969), no. 2, 14–51.CrossRefGoogle Scholar
Ortega, A., On the moduli space of rank 3 vector bundles on a genus 2 curve and the Coble cubic , J. Algebraic Geom. 14 (2005), no. 2), 327–356.CrossRefGoogle Scholar
Pareschi, G. and Popa, M., Regularity on abelian varieties. I , J. Amer. Math. Soc. 16 (2003), no. 2, 285–302.CrossRefGoogle Scholar
Pauly, C., Self-duality of Coble’s quartic hypersurface and applications , Mich. Math. J. 50 (2002), no. 3, 551–574.CrossRefGoogle Scholar
Raynaud, M., Sections des fibrés vectoriels sur une courbe, Bull. Soc. Math. France 110 (1982), no. 1, 103–125.CrossRefGoogle Scholar
van Geemen, B. and Izadi, E., The tangent space to the moduli space of vector bundles on a curve and the singular locus of the theta divisor of the Jacobian , J. Algebraic Geom. 10 (2001), no. 1, 133–177.Google Scholar
Zelaci, H., Moduli spaces of anti-invariant vector bundles over curves and conformal blocks, Ph. D thesis, Université Côte d'Azur, 2017, 1–111.CrossRefGoogle Scholar