No CrossRef data available.
Article contents
ENRIQUES INVOLUTIONS AND BRAUER CLASSES
Published online by Cambridge University Press: 13 December 2022
Abstract
We prove that every element of order 2 in the Brauer group of a complex Kummer surface X descends to an Enriques quotient of X. In generic cases, this gives a bijection between the set 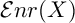 ${\mathcal Enr}(X)$ of Enriques quotients of X up to isomorphism and the set of Brauer classes of X of order 2. For some K3 surfaces of Picard rank
${\mathcal Enr}(X)$ of Enriques quotients of X up to isomorphism and the set of Brauer classes of X of order 2. For some K3 surfaces of Picard rank 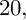 $20,$ we prove that the fibers of
$20,$ we prove that the fibers of 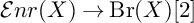 ${\mathcal Enr}(X)\to \mathrm {{Br}}(X)[2]$ above the nonzero points have the same cardinality.
${\mathcal Enr}(X)\to \mathrm {{Br}}(X)[2]$ above the nonzero points have the same cardinality.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal
Footnotes
D.V. was funded by the European Research Council under EU Horizon 2020 research and innovation program grant agreement no. 948066.
References
Balestrieri, F., Berg, J., Manes, M., Park, J., and Viray, B., “
Insufficiency of the Brauer – Manin obstruction for Enriques surfaces
” in Eischen, E.E., Long, L., Pries, R., and Stange, K. (eds.), Directions in number theory, Women Math. Series 3, Springer, Cham, 2016, 1–31.Google Scholar
Beauville, A.,
On the Brauer group of Enriques surfaces
, Math. Res. Lett. 16 (2009), 927–934.CrossRefGoogle Scholar
Brandhorst, S., Sonel, S., and Veniani, D.C., Idoneal genera and K3 surfaces covering an Enriques surface, preprint, arXiv:2003.08914
Google Scholar
Colliot-Thélène, J.-L. and Skorobogatov, A.N., The Brauer–Grothendieck Group, Ergeb. Math. Grenzgeb. (3) 71, Cham: Springer, 2021.CrossRefGoogle Scholar
Garbagnati, A. and Schütt, M.,
Enriques surfaces: Brauer groups and Kummer structures
, Michigan Math. J. 61 (2012) 297–330.CrossRefGoogle Scholar
Harari, D. and Skorobogatov, A.N.,
Non-abelian descent and the arithmetic of Enriques surfaces
, Int. Math. Res. Notices 52 (2005), 3203–3228.CrossRefGoogle Scholar
Horikawa, E.,
On the periods of Enriques surfaces. I, II
, Math. Ann. 234 (1978), 217–246.CrossRefGoogle Scholar
Hulek, K. and Schütt, M.,
Enriques surfaces and Jacobian elliptic K3 surfaces
, Math. Z. 268 (2011), 1025–1056.CrossRefGoogle Scholar
Huybrechts, D., Lectures on K3 Surfaces, Cambridge Stud. Adv. Math. 158, Cambridge: Cambridge University Press, 2016.10.1017/CBO9781316594193CrossRefGoogle Scholar
Keum, J.H.,
Every algebraic Kummer surface is the K3-cover of an Enriques surface
, Nagoya Math. J. 118 (1990), 99–110.CrossRefGoogle Scholar
Nikulin, V.V.,
Integer symmetric bilinear forms and some of their geometric applications
, Izv. Akad. Nauk SSSR Ser. Mat. 43 (1979), 111–177 (in Russian). English translation: Math. USSR-Izv. 14 (1980), 103–167.Google Scholar
Ohashi, H.,
On the number of Enriques quotients of a K3 surface
, Publ. Res. Inst. Math. Sci. 43 (2007), 181–200.10.2977/prims/1199403814CrossRefGoogle Scholar
Ohashi, H.,
Enriques surfaces covered by Jacobian Kummer surfaces
, Nagoya Math. J. 195 (2009), 165–186.CrossRefGoogle Scholar
Sertöz, A.S.,
Which singular K3 surfaces cover an Enriques surface
, Proc. Amer. Math. Soc. 133 (2005), 43–50.CrossRefGoogle Scholar
Shimada, I. and Veniani, D.C.,
Enriques involutions on singular K3 surfaces of small discriminants
, Ann. Sc. Norm. Super. Pisa Cl. Sci. 21 (2020), 1667–1701.Google Scholar
Valloni, D.,
Complex multiplication and Brauer groups of K3 surfaces
, Adv. Math. 385 (2021), art. ID 107772.10.1016/j.aim.2021.107772CrossRefGoogle Scholar
Várilly-Alvarado, A. and Viray, B.,
Failure of the Hasse principle for Enriques surfaces
, Adv. Math. 226 (2011), 4884–4901.CrossRefGoogle Scholar


