No CrossRef data available.
Article contents
Complex Geometry and Electric Double Layers
Published online by Cambridge University Press: 25 February 2011
Abstract
The properties of electric double layers near curved surfaces of arbitrary shape and genus are obtained exactly within the Debye-Hückel theory by means of multiple-scattering expansion. For smooth membranes, geometric and topological feature of the electrostatic free energy then emerge through convergent expansions in inverse powers of the principal radii of curvature. Some consequences for the electrostatic stability of various membrane shapes are considered. We also study the effects of surface singularities, e.g., wedges, on the thermodynamics of electric double layers near a rough colloid. Each wedge yields an additive contribution to the free energy 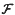 that is a functionof the angle. A probabilistic Brownian representation of
that is a functionof the angle. A probabilistic Brownian representation of 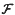 is given, which is entirely similar to that of vibration eigenmodes given by M. Kac long ago in “Canone hear the shape of a drum?” [Amer. Math. Monthly 73S, 1 (1966)]. The analysis yields a universal scaling law for the free energy of a rough colloid with its fractal Minkowski dimension.
is given, which is entirely similar to that of vibration eigenmodes given by M. Kac long ago in “Canone hear the shape of a drum?” [Amer. Math. Monthly 73S, 1 (1966)]. The analysis yields a universal scaling law for the free energy of a rough colloid with its fractal Minkowski dimension.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Materials Research Society 1992

