Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-14T10:24:38.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Tuning transport properties of nickel-doped zinc oxide for thermoelectric applications

Published online by Cambridge University Press:  21 May 2018

Andrei Baranovskiy ,
Ido Koresh  and
Yaron Amouyal
Andrei Baranovskiy
Affiliation:
Department of Materials Science and Engineering, Technion—Israel Institute of Technology, Haifa 32000, Israel
Ido Koresh
Affiliation:
Department of Materials Science and Engineering, Technion—Israel Institute of Technology, Haifa 32000, Israel
Yaron Amouyal*
Affiliation:
Department of Materials Science and Engineering, Technion—Israel Institute of Technology, Haifa 32000, Israel
*
Address all correspondence to Yaron Amouyal at amouyal@technion.ac.il
Get access

Abstract

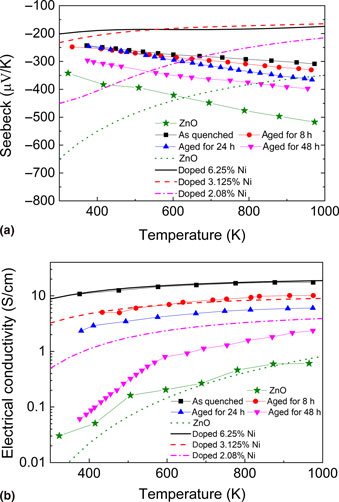
ZnO-based oxides are promising for thermoelectric energy generation at elevated temperatures. We study electrical transport properties of Ni-doped ZnO applying the density functional theory, indicating increase of the electrical conductivity (σ) and decrease of the Seebeck coefficient (S) due to Ni-doping, in full accordance with experimental results. We calculate the temperature-dependent σ and S applying the Boltzmann transport theory, approximating the electron relaxation time, τe. Good agreement with experimental data is obtained considering both temperature and energy dependence of τe. This yields explicit expressions for τe and provides us with powerful predictive tool assessing electronic transport in ZnO.

Type
Research Letters
Information
MRS Communications , Volume 8 , Issue 3 , September 2018 , pp. 858 - 864
Check for updates
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Tritt, T.M. and Subramanian, M.: Thermoelectric materials, phenomena, and applications: a bird's eye view. MRS Bull. 31, 188–229 (2006)Google Scholar
2.Lalonde, A.D., Pei, Y., Wang, H., and Snyder, G.J.: Lead telluride alloy thermoelectrics the opportunity to use solid-state thermoelectrics for waste heat. Mater. Today 14, 526–532 (2011).Google Scholar
3.Liu, W., Hu, J., Zhang, S., Deng, M., and Han, C.: New trends, strategies and opportunities in thermoelectric materials: a perspective. Mater. Today Phys. 1, 50–60 (2017).Google Scholar
4.Koumoto, K., Funahashi, R., Guilmeau, E., Miyazaki, Y., Weidenkaff, A., Wang, Y., and Wan, C.: Thermoelectric ceramics for energy harvesting. J. Am. Ceram. Soc. 96, 1–23 (2013).Google Scholar
5.Koumoto, K., Wang, Y., Zhang, R., Kosuga, A., and Funahashi, R.: Oxide thermoelectric materials: a nanostructuring approach. Annu. Rev. Mater. Res. 40, 363–394 (2010).Google Scholar
6.Terasaki, I., Sasago, Y., and Uchinokura, K.: Large thermoelectric power in NaCo2O4 single crystals. Phys. Rev. B 56, R12685–R12687 (1997).Google Scholar
7.He, J., Liu, Y., and Funahashi, R.: Oxide thermoelectrics: the challenges, progress, and outlook. J. Mater. Res. 26, 1762–1772 (2011).Google Scholar
8.Masset, A., Michel, C., Maignan, A., Hervieu, M., Toulemonde, O., Studer, F., Raveau, B., and Hejtmanek, J.: Misfit-layered cobaltite with an anisotropic giant magnetoresistance: Ca3Co4O9. Phys. Rev. B 62, 166–175 (2000).Google Scholar
9.Amouyal, Y.: On the role of lanthanum substitution defects in reducing lattice thermal conductivity of the AgSbTe2 (P4/mmm) thermoelectric compound for energy conversion applications. Comput. Mater. Sci. 78, 98–103 (2013).Google Scholar
10.Mori, T.: Novel principles and nanostructuring methods for enhanced thermoelectrics. Small 13, 1702013 (2017).Google Scholar
11.Huang, B.-L. and Kaviany, M.: Ab initio and molecular dynamics predictions for electron and phonon transport in bismuth telluride. Phys. Rev. B 77, 1–19 (2008).Google Scholar
12.Martin, R.M.: Electronic Structure. Basic Theory and Practical Methods (Cambridge University Press, Cambridge, UK, 2004).Google Scholar
13.Wiendlocha, B., Kutorasinski, K., Kaprzyk, S., and Tobola, J.: Scripta materialia recent progress in calculations of electronic and transport properties of disordered thermoelectric materials. Scr. Mater. 111, 33–38 (2016).Google Scholar
14.Yaakob, M.K., Hussin, N.H., Taib, M.F.M., Kudin, T.I.T., Hassan, O.H., Ali, A.M.M., and Yahya, M.Z.A.: First principles LDA + U calculations for ZnO materials. Integr. Ferroelectr. 155, 15–22 (2014).Google Scholar
15.Takaki, H., Kobayashi, K., Shimono, M., Kobayashi, N., Hirose, K., Tsujii, N., and Mori, T.: First-principles calculations of Seebeck coefficients in a magnetic. Appl. Phys. Lett. 110, 72107 (2017).Google Scholar
16.Tsujii, N. and Mori, T.: High thermoelectric power factor in a carrier-doped magnetic semiconductor CuFeS_{2}. Appl. Phys. Express 6, 43001 (2013)Google Scholar
17.Iv, V., Janz, E., Gali, A., and Abrikosov, I.A.: Theoretical unification of hybrid-DFT and DFT + U methods for the treatment of localized orbitals. Phys. Rev. B 35146, 1–13 (2014).Google Scholar
18.Koresh, I. and Amouyal, Y.: Effects of microstructure evolution on transport properties of thermoelectric nickel-doped zinc oxide. J. Eur. Ceram. Soc. 37, 3541–3550 (2017)Google Scholar
19.Özgür, Ü, Alivov, Y.I., Liu, C., Teke, A., Reshchikov, M.A., Doğan, S., Avrutin, V., Cho, S., and Morkoç, H.: A comprehensive review of ZnO materials and devices. J. Appl. Phys. 98, 41301 (2005).Google Scholar
20.Ohtaki, M. and Araki, K.: High thermoelectric performance of dually doped ZnO ceramics. J. Electron. Mater. 38, 1234–1238 (2009).Google Scholar
21.Colder, H., Guilmeau, E., Harnois, C., Marinel, S., Retoux, R., and Savary, E.: Preparation of Ni-doped ZnO ceramics for thermoelectric applications. J. Eur. Ceram. Soc. 31, 2957–2963 (2011).Google Scholar
22.Madsen, G.K.H. and Singh, D.J.: BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71 (2006).Google Scholar
23.Kresse, G.: Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).Google Scholar
24.Janotti, A. and Walle, C.G., De, Van, Fundamentals of zinc oxide as a semiconductor. Rep. Prog. Phys. 72, 126501 (2009).Google Scholar
25.Azmin, A., Syafiq, M., Kamil, M., Fariz, M., and Taib, M.: First-principles calculation on electronic properties of zinc oxide by zinc––air system. J. King Saud Univ. Eng. Sci. 29, 278–283 (2015).Google Scholar
26.Mohammadi, A.S.: Density functional approach to study electronic structure of ZnO single crystal. World Appl. Sci. J. 14, 1530–1536 (2011).Google Scholar
27.Von Barth, U. and Hedin, L.: A local exchange-correlation potential for the spin polarized case. J. Phys. C, Solid State Phys. 5, 1629–1642 (2001).Google Scholar
28.Heyd, J., Scuseria, G.E., Ernzerhof, M., Heyd, J., Scuseria, G.E., and Ernzerhof, M.: Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207 (2003).Google Scholar
29.Himmetoglu, B., Floris, A., De Gironcoli, S., and Cococcioni, M.: Hubbard-corrected DFT energy functionals: the LDA + U description of correlated systems. Int. J. Quantum Chem. 114, 14 (2014).Google Scholar
30.Wallace, D.B.: An introduction to Hellmann-Feynman theory. Masters Thesis, University of Central Florida, Orlando, Florida, 2005Google Scholar
31.Baranovskiy, A. and Amouyal, Y.: Dependence of electrical transport properties of CaO(CaMnO3)m (m = 1, 2, 3, ∞) thermoelectric oxides on lattice periodicity. J. Appl. Phys. 121, 65103 (2017).Google Scholar
32.Joseph, E. and Amouyal, Y.: Enhancing thermoelectric performance of PbTe-based compounds by substituting elements: a first principles study. J. Electron. Mater. 44, 1460–1468 (2015).Google Scholar
33.Joseph, E. and Amouyal, Y.: Towards a predictive route for selection of doping elements for the thermoelectric compound PbTe from first-principles. J. Appl. Phys. 117, 175102 (2015).Google Scholar
34.Allen, P.B. and Trivedi, N.: Hall coefficient of cubic metals. Phys. Rev. B 45, 886–890 (1992)Google Scholar
35.Allen, B., Pickett, E., and Krakauer, H.: Anisotropic normal-state transport properties predicted and analyzed for high-T, oxide superconductors. Phys. Rev. B 37, 7482–7490 (1987).Google Scholar
36.Zhang, F.P., Lu, Q.M., Zhang, X., and Zhang, J.X.: Electrical transport properties of CaMnO3 thermoelectric compound: a theoretical study. J. Phys. Chem. Solids 74, 1859–1864 (2013).Google Scholar
37.Wang, Y., Chen, X., Cui, T., Niu, Y., Wang, Y., Wang, M., Ma, Y., and Zou, G.: Enhanced thermoelectric performance of PbTe within the orthorhombic Pnma phase. Phys. Rev. B 76, 155127 (2007).Google Scholar
38.Seeger, K.: Semiconductor Physics Advanced Texts in Physics (Springer-Verlag Heidelberg GmbH, Berlin 2004).Google Scholar
39.Hao, S., Shi, F., Dravid, V., Kanatzidis, M., and Wolverton, C.: Computational prediction of high thermoelectric performance in hole doped layered GeSe. Chem. Mater. 28, 3218–3226 (2016).Google Scholar
40.Bouzerar, G., Thébaud, S., Adessi, C., Debord, R., Apreutesei, M., Bachelet, R., and Pailhès, S.: Unified modelling of the thermoelectric properties in SrTiO3. arXiv:1702.02751 [cond-mat.mtrl-sci]. 1–5 (2017).Google Scholar
41.Brida, D., Gadermaier, C., Polli, D., Kabanov, V.V., Mihailovic, D., and Cerullo, G.: Electron relaxation in metals and high-Tc superconductors on the 10-fs timescale. In Ultrafast Phenomena in Semiconductors and Nanostructure Materials XV, Tsen, K.-T., Song, J.-J., Betz, M. and Elezzabi, A.Y. eds.; 2011; pp. 1–7.Google Scholar
42.Bennemann, K.H.: Ultrafast dynamics in solids. J. Phys. Condens. Matter 16, R995–R1056 (2004).Google Scholar
43.Ahmed, F. and Tsujii, N.: Thermoelectric properties of CuGa1−xMnxTe2: power factor enhancement by incorporation of magnetic ions. J. Mater. Chem. A 5, 7545–7554 (2017).Google Scholar
44.Khan, A.U., Al, R., Al, R., Pakdel, A., Vaney, J., Fontaine, B., Mitani, S., and Mori, T.: Sb doping of metallic CuCr2S4 as a route to highly improved thermoelectric properties. Chem. Mater. 29, 2988 (2017).Google Scholar
45.Takaki, H., Kobayashi, K., Shimono, M., Kobayashi, N., Hirose, K., Tsujii, N., and Mori, T.: Thermoelectric properties of a magnetic semiconductor CuFeS2. Mater. Today Phys. J. 3, 85–92 (2017).Google Scholar
46.Kowalczyk, A., Falkowski, M., and Toliński, T.: Thermal conductivity and Lorenz number of the Ce1−xLaxNiAl4 Kondo alloys. Solid State Commun. 193, 26–29 (2014).Google Scholar