Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-13T14:29:57.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Investigation of thermal transport properties of copper-supported pillared-graphene structure using molecular dynamics simulations

Published online by Cambridge University Press:  18 November 2020

Khaled Almahmoud ,
Thiruvillamalai Mahadevan ,
Jincheng Du ,
Huseyin Bostanci  and
Weihuan Zhao
Khaled Almahmoud
Affiliation:
Mechanical Engineering Department, University of North Texas, Denton, TX76207, USA
Thiruvillamalai Mahadevan
Affiliation:
Materials Science and Engineering Department, University of North Texas, Denton, TX76207, USA
Jincheng Du
Affiliation:
Materials Science and Engineering Department, University of North Texas, Denton, TX76207, USA
Huseyin Bostanci
Affiliation:
Mechanical Engineering Department, University of North Texas, Denton, TX76207, USA
Weihuan Zhao*
Affiliation:
Mechanical Engineering Department, University of North Texas, Denton, TX76207, USA
*
Address all correspondence to Weihuan Zhao at weihuan.zhao@unt.edu
Get access

Abstract

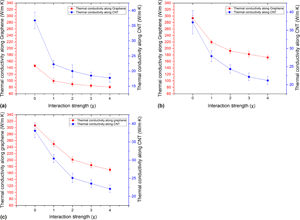
Thermal transport of pillared-graphene structure (PGS) supported on a copper substrate was investigated using equilibrium molecular dynamics. The results show that thermal conductivity along the graphene sheet in Cu-supported PGS ranges between 96.12 and 247.16 W/m K for systems with different dimensions at an interaction strength χ = 1. Thermal conductivity along carbon nanotube was found to range between 22.43 and 30.83 W/m K. The increase of interaction strength between Cu and carbon leads to a general decrease in thermal conductivity of PGS. The simulation results suggest that the thermal conductivity in Cu-supported PGS systems is governed by system geometry and phonon transport.

Type
Research Letters
Information
MRS Communications , Volume 10 , Issue 4 , December 2020 , pp. 695 - 701
Check for updates
Copyright
Copyright © The Author(s), 2020, published on behalf of Materials Research Society by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Varshney, V., Patnaik, S.S., Roy, A.K., Froudakis, G., and Farmer, B.L.: Modeling of thermal transport in pillared-graphene architectures. ACS Nano 4, 1153–1161 (2010).CrossRefGoogle ScholarPubMed
Chen, L. and Kumar, S.: Thermal transport in graphene supported on copper. J. Appl. Phys. 112, 043502 (2012).CrossRefGoogle Scholar
Pop, E., Varshney, V., and Roy, A.K.: Thermal properties of graphene: fundamentals and applications. MRS Bull. 37, 1273–1281 (2012).CrossRefGoogle Scholar
Balandin, A.A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., and Lau, C.N.: Superior thermal conductivity of single-layer graphene. Nano Lett. 8, 902–907 (2008).CrossRefGoogle ScholarPubMed
Kostogrud, I.A., Boyko, E.V., and Smovzh, D.V.: The main sources of graphene damage at transfer from copper to PET/EVA polymer. Mater. Chem. Phys. 2019, 67–73 (2018).CrossRefGoogle Scholar
Li, X., Cai, W., An, J., Kim, S., Nah, J., Yang, D., Piner, R., Velamakanni, A., Jung, I., Tutuc, E., Banerjee, S.K., Colombo, L., and Ruoff, R.S.: Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 324, 1312–1314 (2009).CrossRefGoogle ScholarPubMed
Won Sun, J., Kitt, A., Magnuson, C.W., Hao, Y., Ahmed, S., An, J., Swan, A.K., Goldberg, B.B., and Ruoff, R.S.: Transfer of CVD-grown monolayer graphene onto arbitrary substrates. ACS Nano 5, 6916–6924 (2011).Google Scholar
Hun Seol, J., Jo, I., Moore, A.L., Lindsay, L., Aitken, Z.H., Pettes, M.T., Li, X., Yao, Z., Huang, R., Broido, D., Mingo, N., Ruoff, R.S., and Shi, L.: Two-dimensional phonon transport in supported graphene. Science 328, 213–216 (2010).CrossRefGoogle Scholar
Ghosh, S., Calizo, I., Teweldebrhan, D., Pokatilov, E.P., Nika, D.L., Balandin, A.A., Bao, W., Miao, F., and Ning Lao, C.: Extremely high thermal conductivity of graphene: prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 92, 151911 (2008).CrossRefGoogle Scholar
Nika, D.L., Pokatilov, E.P., Askerov, A.S., and Balandin, A.A.: Phonon thermal conduction in graphene: role of Umklapp and edge roughness scattering. Phys. Rev. B 79, 155413 (2009).CrossRefGoogle Scholar
Lindsay, L., Broido, D.A., and Mingo, N.: Flexural phonons and thermal transport in graphene. Phys. Rev. B 82, 115427 (2010).CrossRefGoogle Scholar
Niu, J., Li, M., Choi, W., Dai, L., and Xia, Z.: Growth of junctions in 3D carbon nanotube-graphene nanostructures: a quantum mechanical molecular dynamics study. Carbon 67, 627–634 (2013).CrossRefGoogle Scholar
Loh, G.C., Teo, E.H.T., and Tay, B.K.: Interpillar phononics in pillared-graphene hybrid nanostructures. J. Appl. Phys. 110, 083502 (2011).CrossRefGoogle Scholar
Park, J. and Prakash, V.: Phonon scattering and thermal conductivity of pillared-graphene structures with carbon nanotube-graphene intramolecular junctions. J. Appl. Phys. 116, 014303 (2014).CrossRefGoogle Scholar
Almahmoud, K., Mahadevan, T., Barhemmati-Rajab, N., Du, J., Bostanci, H., and Zhao, W.: Investigation of thermal transport properties in pillared-graphene structure using non-equilibrium molecular dynamics simulations. MRS Commun 10, 506–511 (2020).CrossRefGoogle Scholar
Gonzalez, M.A.: Force fields and molecular dynamics simulations. EDP Sci. 12, 169–200 (2011).Google Scholar
Lindsay, L. and Broido, D.A.: Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 81, 205441 (2010).CrossRefGoogle Scholar
Daw, M.S. and Baskes, M.I.: Embedded-atom method: derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 29, 6443–6543 (1984).CrossRefGoogle Scholar
Xu, Z. and Buehler, M.J.: Nanoengineering heat transfer performance at carbon nanotube interfaces. ACS Nano 3, 2767–2775 (2009).CrossRefGoogle ScholarPubMed
Schelling, P.K., Phillpot, S.R., and Keblinski, P.: Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 65, 144306 (2002).CrossRefGoogle Scholar
Barhemmati-Rajab, N., Mahadevan, T., Du, J., and Zhao, W.: Thermal transport properties enhancement of paraffin via encapsulation into boron nitride nanotube: a molecular dynamics study. MRS Commun 10, 475–481 (2020).CrossRefGoogle Scholar
Javanmardi, M.J. and Jafarpur, K.: A molecular dynamics simulation for thermal conductivity evaluation of carbon nanotube-water nanofluids. J. Heat Transfer 135, 042401 (2013).CrossRefGoogle Scholar
McGaughey, A.J.H. and Kaviany, M.: Phonon transport in molecular dynamics simulations: formulation and thermal conductivity prediction. Adv. Heat Transfer 39, 169–255 (2006).CrossRefGoogle Scholar
Khan, A., Navid, I., Noshin, M., Uddin, H., Hossain, F., and Subrina, S.: Equilibrium molecular dynamics (MD) simulation study of thermal conductivity of graphene nanoribbon: a comparative study on MD potentials. Electronics 4, 1109–1124 (2015).CrossRefGoogle Scholar
Yang, D., Ma, F., Sun, Y., Hu, T., and Xu, K.: Influence of typical defects on thermal conductivity of graphene nanoribbons: an equilibrium molecular dynamics simulation. Appl. Surf. Sci. 258, 9926–9931 (2012).CrossRefGoogle Scholar
Zhang, W., Zhu, Z., Wang, F., Wang, T., Sun, L., and Wang, Z.: Chirality dependence of the thermal conductivity of carbon nanotubes. Nanotechnology 15, 936–939 (2004).CrossRefGoogle Scholar
Zhang, H., Lee, G., and Cho, K.: Thermal transport in graphene and effect of vacancy defects. Phys. Rev. B 84, 115460 (2011).CrossRefGoogle Scholar
Ye, Z.-Q., Cao, B.-Y., Yao, W.-J., Feng, T., and Ruan, X.: Spectral phonon thermal properties in graphene nanoribbons. Carbon 93, 915–923 (2015).CrossRefGoogle Scholar
Mahdizadeh, S.J. and Goharshadi, E.K.: Thermal conductivity and heat transport properties of graphene nanoribbons. J. Nanopart. Res. 16, 2553 (2014).CrossRefGoogle Scholar
Khadem, M.H. and Wemhoff, A.P.: Comparison of Green-Kubo and NEMD heat flux formulations for thermal conductivity prediction using the Tersoff potential. Comput. Mater. Sci. 69, 428–434 (2013).CrossRefGoogle Scholar
Ikeshoji, T. and Hafskjold, B.: Non-equilibrium molecular dynamics calculation of heat conduction in liquid and through liquid-gas interface. Mol. Phys. 81, 251–261 (1994).CrossRefGoogle Scholar
Wirnsberger, P., Frenkel, D., and Dellago, C.: An enhanced version of the heat exchange algorithm with excellent energy conservation properties. J. Chem. Phys. 143, 124104 (2015).CrossRefGoogle ScholarPubMed
Müller-Plathe, F. and Bordat, P.: A simple non-equilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 106, 310–326 (1997).CrossRefGoogle Scholar
Haskins, J., Kinaci, A., Sevik, C., Sevincli, H., Cuniberti, G., and Cagin, T.: Control of thermal and electronic transport in defect-engineered graphene nanoribbons. ACS Nano 5, 3779–3789 (2011).CrossRefGoogle ScholarPubMed
Landry, E.S., Hussein, M.I., and McGaughey, A.J.H.: Complex superlattice unit cell designs for reduced thermal conductivity. Phys. Rev. B 77, 184302 (2008).CrossRefGoogle Scholar
Materials And Processes Simulations Platform (Scienomics SARL, Version 4.3, Paris, France).Google Scholar
Shahsavari, R. and Sakhavand, N.: Junction configuration-induced mechanisms govern elastic and inelastic deformations in hybrid carbon nanomaterials. Carbon 95, 699–709 (2015).CrossRefGoogle Scholar
Ong, Z.-Y. and Pop, E.: Molecular dynamics simulation of thermal boundary conductance between carbon nanotubes and SiO2. Phys. Rev. B 81, 155408 (2010).CrossRefGoogle Scholar
Mohsin, K.M., Srivastaa, A., Sharma, A.K., Mayberry, C., and Fahad, M.S.: Current transport in graphene/copper hybrid nanoribbon interconnect: a first principle study. ECS Trans. 75, 49–53 (2016).CrossRefGoogle Scholar
Berber, S., Kwon, Y.-K., and Tomanek, D.: Unusually high thermal conductivity of carbon nanotubes. Phys. Rev. Lett. 84, 4613–4616 (2000).CrossRefGoogle ScholarPubMed
Sellan, D.P., Landry, E.S., Turney, J.E., McGaughey, J.H., and Amon, C.H.: Size effects in molecular dynamics thermal conductivity predictions. Phys. Rev. B 81, 214305 (2010).CrossRefGoogle Scholar