Article contents
Experimental determination of phonon thermal conductivity and Lorenz ratio of single-crystal bismuth telluride
Published online by Cambridge University Press: 25 October 2017
Abstract
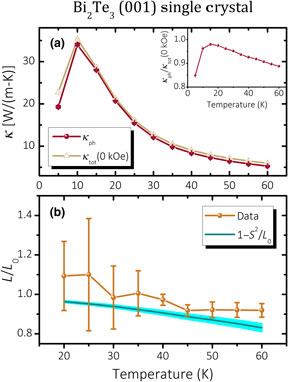
We use a magnetothermal resistance method to measure the lattice thermal conductivity of single-crystal Bi2Te3 from 5 to 60 K. Lattice thermal conductivity is calculated by extrapolating the thermal conductivity versus electrical conductivity curve to a zero electrical conductivity value. Our results show that the measured phonon thermal conductivity follows the  ${\rm e}^{{\it\Delta} _{{\rm min}}/T}$ temperature dependence and the Lorenz ratio corresponds to the modified Sommerfeld value in the intermediate temperature range. Our low-temperature experimental data and analysis on Bi2Te3 are a complement to previous measurements of Goldsmid (Ref. 17) and theoretical calculations by Hellman et al. (Ref. 18) at higher temperature 100–300 K.
${\rm e}^{{\it\Delta} _{{\rm min}}/T}$ temperature dependence and the Lorenz ratio corresponds to the modified Sommerfeld value in the intermediate temperature range. Our low-temperature experimental data and analysis on Bi2Te3 are a complement to previous measurements of Goldsmid (Ref. 17) and theoretical calculations by Hellman et al. (Ref. 18) at higher temperature 100–300 K.
Information
- Type
- Research Letters
- Information
- Copyright
- Copyright © Materials Research Society 2017
References
- 7
- Cited by


