Hostname: page-component-7dd5485656-6kn8j Total loading time: 0 Render date: 2025-10-31T20:10:31.015Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of gravity in the Cassie-to-Wenzel transition on a micropatterned surface

Published online by Cambridge University Press:  13 December 2019

Arash Azimi  and
Ping He Open the ORCID record for Ping He [Opens in a new window]
Arash Azimi
Affiliation:
Department of Mechanical Engineering, Lamar University, Beaumont, TX77710, USA
Ping He*
Affiliation:
Department of Mechanical Engineering, Lamar University, Beaumont, TX77710, USA
*
Address all correspondence to Ping He at phe@lamar.edu
Get access

Abstract

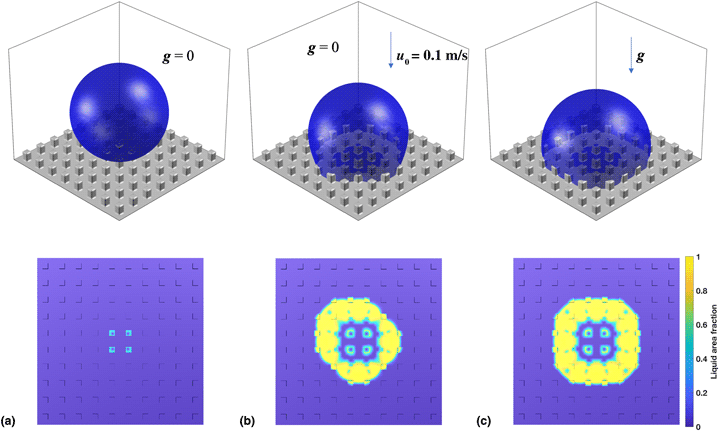
When the Cassie–Baxter and Wenzel states coexist for a liquid droplet on a micropatterned surface, the Cassie-to-Wenzel transition takes place if the energy barrier is overcome. Although multiple metastable states coexist due to the micropattern, this paper presents a simple Cassie-to-Wenzel transition of a 2 µL water droplet on a particular micropillared surface: When the droplet is gently deposited above the surface, it equalizes to the Cassie state at zero gravity; however, it transitions to the Wenzel state at the terrestrial gravity, in which the gravitational potential energy overcomes the energy barrier between the Cassie and Wenzel states.

Information

Type
Research Letters
Information
MRS Communications , Volume 10 , Issue 1 , March 2020 , pp. 129 - 134
Check for updates
Copyright
Copyright © Materials Research Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Wenzel, R.N.: Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 28, 988 (1936).CrossRefGoogle Scholar
2.Cassie, A.B.D. and Baxter, S.: Wettability of porous surfaces. Trans. Faraday Soc. 40, 0546 (1944).CrossRefGoogle Scholar
3.Kawai, A. and Nagata, H.: Wetting behavior of liquid on geometrical rough-surface formed by photolithography. Jpn. J. Appl. Phys. 33, L1283 (1994).CrossRefGoogle Scholar
4.Bico, J., Marzolin, C., and Quere, D.: Pearl drops. Europhys. Lett. 47, 220 (1999).CrossRefGoogle Scholar
5.Patankar, N.A.: On the modeling of hydrophobic contact angles on rough surfaces. Langmuir 19, 1249 (2003).CrossRefGoogle Scholar
6.He, B., Patankar, N.A., and Lee, J.: Multiple equilibrium droplet shapes and design criterion for rough hydrophobic surfaces. Langmuir 19, 4999 (2003).CrossRefGoogle Scholar
7.Patankar, N.A.: Transition between superhydrophobic states on rough surfaces. Langmuir 20, 7097 (2004).CrossRefGoogle ScholarPubMed
8.Whyman, G. and Bormashenko, E.: Wetting transitions on rough substrates: general considerations. J. Adhes. Sci. Technol. 26, 207 (2012).CrossRefGoogle Scholar
9.Patankar, N.A.: Consolidation of hydrophobic transition criteria by using an approximate energy minimization approach. Langmuir 26, 8941 (2010).CrossRefGoogle ScholarPubMed
10.Pashos, G., Kokkoris, G., and Boudouvis, A.G.: Minimum energy paths of wetting transitions on grooved surfaces. Langmuir 31, 3059 (2015).CrossRefGoogle ScholarPubMed
11.Guo, H.Y., Li, B., and Feng, X.Q.: Stability of Cassie-Baxter wetting states on microstructured surfaces. Phys. Rev. E 94, 042801 (2016).CrossRefGoogle ScholarPubMed
12.Liu, T.Q., Li, Y.J., Li, X.Q., and Sun, W.: Theoretical analysis of droplet transition from Cassie to Wenzel state. Chinese Phys. B 24, 116801 (2015).CrossRefGoogle Scholar
13.Liu, T.Q., Li, Y.J., Li, X.Q., and Sun, W.: Mechanism Study on transition of Cassie droplets to Wenzel State after meniscus touching substrate of pillars. J. Phys. Chem. C 121, 9802 (2017).CrossRefGoogle Scholar
14.Rohrs, C.J., Azimi, A., and He, P.: Wetting on micropatterned surfaces: partial penetration in the Cassie State and Wenzel deviation theoretically explained. Langmuir 35, 15421 (2019).CrossRefGoogle ScholarPubMed
15.Koishi, T., Yasuoka, K., Fujikawa, S., Ebisuzaki, T., and Zeng, X.C.: Coexistence and transition between Cassie and Wenzel state on pillared hydrophobic surface. Proc. Natl. Acad. Sci. USA 106, 8435 (2009).CrossRefGoogle ScholarPubMed
16.Gong, W., Zu, Y.Q., Chen, S., and Yan, Y.Y.: Wetting transition energy curves for a droplet on a square-post patterned surface. Sci. Bull. 62, 136 (2017).CrossRefGoogle Scholar
17.Lee, J.S., Moon, J.Y., and Lee, J.S.: Study of transporting of droplets on heterogeneous surface structure using the lattice Boltzmann approach. Appl. Therm. Eng. 72, 104 (2014).CrossRefGoogle Scholar
18.Zhang, W., Zhang, R.R., Jiang, C.G., and Wu, C.W.: Effect of pillar height on the wettability of micro-textured surface: volume-of-fluid simulations. Int. J. Adhes. Adhes. 74, 64 (2017).CrossRefGoogle Scholar
19.Azimi, A., He, P., Rohrs, C., and Yao, C.W.: Developing a novel continuum model of static and dynamic contact angles in a case study of a water droplet on micro-patterned hybrid substrates. MRS Commun. 8, 1445 (2018).CrossRefGoogle Scholar
20.He, P. and Yao, C.W.: Simulating contact angle hysteresis using pseudo-line tensions. MRS Commun. 9, 1060 (2019).CrossRefGoogle Scholar

Azimi and He supplementary material

Azimi and He supplementary material 1

Download Azimi and He supplementary material(Video)
Video 3.8 MB

Azimi and He supplementary material

Azimi and He supplementary material 2

Download Azimi and He supplementary material(Video)
Video 7.4 MB

Azimi and He supplementary material

Azimi and He supplementary material 3

Download Azimi and He supplementary material(Video)
Video 7.7 MB