Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Diestel, Reinhard
Halin, Rudolf
and
Vogler, Walter
1985.
Some remarks on universal graphs.
Combinatorica,
Vol. 5,
Issue. 4,
p.
283.
Komjáth, Peter
Mekler, Alan H.
and
Pach, János
1988.
Some universal graphs.
Israel Journal of Mathematics,
Vol. 64,
Issue. 2,
p.
158.
Nešetřil, Jaroslav
and
Rödl, Vojtěch
1989.
Chromatically optimal rigid graphs.
Journal of Combinatorial Theory, Series B,
Vol. 46,
Issue. 2,
p.
133.
Diestel, Reinhard
1989.
Simplicial decompositions of graphs: a survey of applications.
Discrete Mathematics,
Vol. 75,
Issue. 1-3,
p.
121.
Komjáth, Péter
and
Pach, János
1991.
Universal elements and the complexity of certain classes of infinite graphs.
Discrete Mathematics,
Vol. 95,
Issue. 1-3,
p.
255.
Cherlin, G.
and
Komjáth, P.
1994.
There is no universal countable pentagon‐free graph.
Journal of Graph Theory,
Vol. 18,
Issue. 4,
p.
337.
Komj�th, P.
and
Pach, J.
1994.
The complexity of a class of infinite graphs.
Combinatorica,
Vol. 14,
Issue. 1,
p.
121.
F�redi, Z.
and
Komj�th, P.
1997.
Nonexistence of universal graphs without some trees.
Combinatorica,
Vol. 17,
Issue. 2,
p.
163.
Cherlin, Gregory
Shelah, Saharon
and
Shi, Niandong
1999.
Universal Graphs with Forbidden Subgraphs and Algebraic Closure.
Advances in Applied Mathematics,
Vol. 22,
Issue. 4,
p.
454.
Nešetřil, Jaroslav
and
Shelah, Saharon
2003.
On the order of countable graphs.
European Journal of Combinatorics,
Vol. 24,
Issue. 6,
p.
649.
Cherlin, Gregory
and
Shelah, Saharon
2007.
Universal graphs with a forbidden subtree.
Journal of Combinatorial Theory, Series B,
Vol. 97,
Issue. 3,
p.
293.
Cherlin, Gregory
and
Tallgren, Lasse
2007.
Universal graphs with a forbidden near‐path or 2‐bouquet.
Journal of Graph Theory,
Vol. 56,
Issue. 1,
p.
41.
Cherlin, Gregory
2011.
Forbidden substructures and combinatorial dichotomies: WQO and universality.
Discrete Mathematics,
Vol. 311,
Issue. 15,
p.
1543.
Shelah, Saharon
2012.
Universality among graphs omitting a complete bipartite graph.
Combinatorica,
Vol. 32,
Issue. 3,
p.
325.
ATMINAS, AISTIS
LOZIN, VADIM V.
KITAEV, SERGEY
and
VALYUZHENICH, ALEXANDR
2013.
UNIVERSAL GRAPHS AND UNIVERSAL PERMUTATIONS.
Discrete Mathematics, Algorithms and Applications,
Vol. 05,
Issue. 04,
p.
1350038.
Komjáth, Péter
and
Shelah, Saharon
2019.
Universal graphs omitting finitely many finite graphs.
Discrete Mathematics,
Vol. 342,
Issue. 12,
p.
111596.
Shelah, Saharon
2021.
Divide and Conquer: Dividing Lines and Universality.
Theoria,
Vol. 87,
Issue. 2,
p.
259.
Lehner, Florian
2023.
A note on classes of subgraphs of locally finite graphs.
Journal of Combinatorial Theory, Series B,
Vol. 161,
Issue. ,
p.
52.

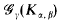 denote the class of all graphs on γ vertices having no subgraph isomorphic to
denote the class of all graphs on γ vertices having no subgraph isomorphic to 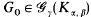 is called universal if every
is called universal if every 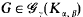 can be embedded into
can be embedded into 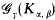 has a universal element, if, and only if, (i) γ >
has a universal element, if, and only if, (i) γ > 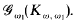 .
.