Published online by Cambridge University Press: 29 November 2017
Combinatorial discrepancy is a complexity measure of a collection of sets which quantifies how well the sets in the collection can be simultaneously balanced. More precisely, we are given an  $n$-point set
$n$-point set 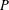 $P$, and a collection
$P$, and a collection 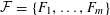 ${\mathcal{F}}=\{F_{1},\ldots ,F_{m}\}$ of subsets of
${\mathcal{F}}=\{F_{1},\ldots ,F_{m}\}$ of subsets of 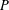 $P$, and our goal is color
$P$, and our goal is color 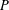 $P$ with two colors, red and blue, so that the maximum over the
$P$ with two colors, red and blue, so that the maximum over the 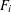 $F_{i}$ of the absolute difference between the number of red elements and the number of blue elements (the discrepancy) is minimized. Combinatorial discrepancy has many applications in mathematics and computer science, including constructions of uniformly distributed point sets, and lower bounds for data structures and private data analysis algorithms. We investigate the combinatorial discrepancy of geometrically defined systems, in which
$F_{i}$ of the absolute difference between the number of red elements and the number of blue elements (the discrepancy) is minimized. Combinatorial discrepancy has many applications in mathematics and computer science, including constructions of uniformly distributed point sets, and lower bounds for data structures and private data analysis algorithms. We investigate the combinatorial discrepancy of geometrically defined systems, in which 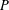 $P$ is an
$P$ is an  $n$-point set in
$n$-point set in 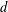 $d$-dimensional space, and
$d$-dimensional space, and 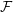 ${\mathcal{F}}$ is the collection of subsets of
${\mathcal{F}}$ is the collection of subsets of  $P$ induced by dilations and translations of a fixed convex polytope
$P$ induced by dilations and translations of a fixed convex polytope 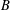 $B$. Such set systems include systems of sets induced by axis-aligned boxes, whose discrepancy is the subject of the well-known Tusnády problem. We prove new discrepancy upper and lower bounds for such set systems by extending the approach based on factorization norms previously used by the author, Matoušek, and Talwar. We also outline applications of our results to geometric discrepancy, data structure lower bounds, and differential privacy.
$B$. Such set systems include systems of sets induced by axis-aligned boxes, whose discrepancy is the subject of the well-known Tusnády problem. We prove new discrepancy upper and lower bounds for such set systems by extending the approach based on factorization norms previously used by the author, Matoušek, and Talwar. We also outline applications of our results to geometric discrepancy, data structure lower bounds, and differential privacy.