Article contents
SPECTRAL THEORETIC CHARACTERIZATION OF THE MASSLESS DIRAC ACTION
Published online by Cambridge University Press: 08 March 2016
Abstract
We consider an elliptic self-adjoint first-order differential operator 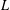 $L$ acting on pairs (2-columns) of complex-valued half-densities over a connected compact three-dimensional manifold without boundary. The principal symbol of the operator
$L$ acting on pairs (2-columns) of complex-valued half-densities over a connected compact three-dimensional manifold without boundary. The principal symbol of the operator 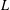 $L$ is assumed to be trace-free and the subprincipal symbol is assumed to be zero. Given a positive scalar weight function, we study the weighted eigenvalue problem for the operator
$L$ is assumed to be trace-free and the subprincipal symbol is assumed to be zero. Given a positive scalar weight function, we study the weighted eigenvalue problem for the operator 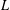 $L$ . The corresponding counting function (number of eigenvalues between zero and a positive
$L$ . The corresponding counting function (number of eigenvalues between zero and a positive  $\unicode[STIX]{x1D706}$ ) is known to admit, under appropriate assumptions on periodic trajectories, a two-term asymptotic expansion as
$\unicode[STIX]{x1D706}$ ) is known to admit, under appropriate assumptions on periodic trajectories, a two-term asymptotic expansion as 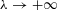 $\unicode[STIX]{x1D706}\rightarrow +\infty$ and we have recently derived an explicit formula for the second asymptotic coefficient. The purpose of this paper is to establish the geometric meaning of the second asymptotic coefficient. To this end, we identify the geometric objects encoded within our eigenvalue problem—metric, non-vanishing spinor field and topological charge—and express our asymptotic coefficients in terms of these geometric objects. We prove that the second asymptotic coefficient of the counting function has the geometric meaning of the massless Dirac action.
$\unicode[STIX]{x1D706}\rightarrow +\infty$ and we have recently derived an explicit formula for the second asymptotic coefficient. The purpose of this paper is to establish the geometric meaning of the second asymptotic coefficient. To this end, we identify the geometric objects encoded within our eigenvalue problem—metric, non-vanishing spinor field and topological charge—and express our asymptotic coefficients in terms of these geometric objects. We prove that the second asymptotic coefficient of the counting function has the geometric meaning of the massless Dirac action.
Information
- Type
- Research Article
- Information
- Creative Commons
- This article is distributed with Open Access under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided that the original work is properly cited.
- Copyright
- Copyright © University College London 2016
References
- 1
- Cited by

