Hostname: page-component-cb9f654ff-mwwwr Total loading time: 0 Render date: 2025-08-10T15:14:27.150Z Has data issue: false hasContentIssue false
  • English
  • Français

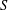$S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES

Part of: Diophantine approximation, transcendental number theory Sequences and sets

Published online by Cambridge University Press:  29 November 2017

Yann Bugeaud  and
Jan-Hendrik Evertse
Yann Bugeaud
Affiliation:
Université de Strasbourg, CNRS, IRMA UMR 7501, 7, rue René Descartes, 67000 Strasbourg, France email bugeaud@math.u-strasbg.fr
Jan-Hendrik Evertse
Affiliation:
Universiteit Leiden, Mathematisch Instituut, Postbus 9512, 2300 RA Leiden, The Netherlands email evertse@math.leidenuniv.nl
Get access

Abstract

Let 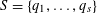$S=\{q_{1},\ldots ,q_{s}\}$ be a finite, non-empty set of distinct prime numbers. For a non-zero integer 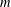$m$ , write 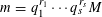$m=q_{1}^{r_{1}}\cdots q_{s}^{r_{s}}M$ , where 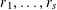$r_{1},\ldots ,r_{s}$ are non-negative integers and 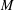$M$ is an integer relatively prime to 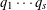$q_{1}\cdots q_{s}$ . We define the 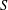$S$ -part 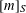$[m]_{S}$ of 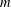$m$ by 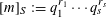$[m]_{S}:=q_{1}^{r_{1}}\cdots q_{s}^{r_{s}}$ . Let 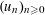$(u_{n})_{n\geqslant 0}$ be a linear recurrence sequence of integers. Under certain necessary conditions, we establish that for every 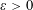$\unicode[STIX]{x1D700}>0$ , there exists an integer 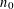$n_{0}$ such that 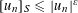$[u_{n}]_{S}\leqslant |u_{n}|^{\unicode[STIX]{x1D700}}$ holds for 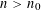$n>n_{0}$ . Our proof is ineffective in the sense that it does not give an explicit value for 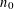$n_{0}$ . Under various assumptions on 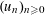$(u_{n})_{n\geqslant 0}$ , we also give effective, but weaker, upper bounds for 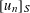$[u_{n}]_{S}$ of the form 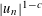$|u_{n}|^{1-c}$ , where $c$ is positive and depends only on 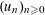$(u_{n})_{n\geqslant 0}$ and 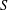$S$ .

MSC classification

Primary: 11B37: Recurrences 11J86: Linear forms in logarithms; Baker's method 11J87: Schmidt Subspace Theorem and applications

Information

Type
Research Article
Information
Mathematika , Volume 63 , Issue 3 , 2017 , pp. 840 - 851
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bugeaud, Y., Evertse, J.-H. and Győry, K., $S$ -parts of values of univariate polynomials, binary forms and decomposable forms at integral points. Preprint, 2017, arXiv:1708.08290 [math.NT].Google Scholar
Evertse, J.-H., On sums of S-units and linear recurrences. Compos. Math. 53 1984, 225–244.Google Scholar
Evertse, J.-H. and Győry, K., Unit Equations in Diophantine Number Theory, Cambridge University Press (Cambridge, 2015).Google Scholar
Gross, S. S. and Vincent, A. F., On the factorization of f (n) for f (x) in Z[x]. Int. J. Number Theory 9 2013, 1225–1236.Google Scholar
Luca, F. and Mignotte, M., Arithmetic properties of the integer part of the powers of an algebraic number. Glas. Mat. Ser. III 44 2009, 285–307.Google Scholar
Mahler, K., Eine arithmetische Eigenschaft der rekurrierenden Reihen. Mathematica (Zutphen) 3 1934, 153–156.Google Scholar
Mahler, K., A remark on recursive sequences. J. Math. Sci. Delhi 1 1966, 12–17.Google Scholar
Matveev, E. M., An Explicit Lower Bound for a Homogeneous Rational Linear form in Logarithms of Algebraic Numbers. II, (Izv. Ross. Acad. Nauk Ser. Mat. 64 ) (2000), 125–180 (in Russian); English translation in Izv. Math. 64 (2000), 1217–1269.Google Scholar
van der Poorten, A. J. and Schlickewei, H. P., The growth condition for recurrence sequences. Macquarie University Math. Report 82-0041 (1982).Google Scholar
Ridout, D., The p-adic generalization of the Thue–Siegel–Roth theorem. Mathematika 5 1958, 40–48.Google Scholar
Shorey, T. N. and Tijdeman, R., Exponential Diophantine Equations (Cambridge Tracts in Mathematics 87 ), Cambridge University Press (Cambridge, 1986).Google Scholar
Stewart, C. L., On divisors of terms of linear recurrence sequences. J. Reine Angew. Math. 333 1982, 12–31.Google Scholar
Stewart, C. L., On the greatest square-free factor of terms of a linear recurrence sequence. In Diophantine Equations (Tata Institute of Fundamental Research Studies in Mathematics 20 ), Tata Institute of Fundamental Research (Mumbai, 2008), 257–264.Google Scholar
Stewart, C. L., On divisors of Lucas and Lehmer numbers. Acta Math. 211 2013, 291–314.Google Scholar
Stewart, C. L., On prime factors of terms of linear recurrence sequences. In Number Theory and Related Fields (Springer Proceedings in Mathematics & Statistics 43 ), Springer (New York, 2013), 341–359.Google Scholar
Yu, K., p-adic logarithmic forms and group varieties. III. Forum Math. 19 2007, 187–280.Google Scholar