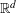Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baier, Stephan
2017.
Diophantine approximation on lines in $$\mathbb {C}^2$$ C 2 with Gaussian prime constraints.
European Journal of Mathematics,
Vol. 3,
Issue. 3,
p.
614.
Baier, Stephan
and
Ghosh, Anish
2018.
Inhomogeneous diophantine approximation with prime constraints.
Proceedings - Mathematical Sciences,
Vol. 128,
Issue. 4,
Harrap, Stephen
Hussain, Mumtaz
and
Kristensen, Simon
2018.
A problem in non-linear Diophantine approximation.
Nonlinearity,
Vol. 31,
Issue. 5,
p.
1734.
Oliveira, André P.
2022.
Khintchine’s theorem with rationals coming from neighborhoods in different places.
International Journal of Number Theory,
Vol. 18,
Issue. 06,
p.
1367.