Article contents
A presentation of SL2 for Euclidean imaginary quadratic number fields
Published online by Cambridge University Press: 26 February 2010
Extract
Let G be any group and G′ its derived, then G/G′—the group G made abelian—will be denoted by Ga. Over any ring R, denote by E2(R) the group generated by the matrices 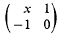 as x ranges over R; the structure of E2(R)a has been described in a recent theorem [2; Th. 9.3] for certain rings R, the “quasi-free rings for GE2” (cf. §2 below). Now over a commutative Euclidean domain, E2(R) is just the special linear group SL2(R); this suggests applying the theorem to the ring of integers in a Euclidean number field. However, the only number fields whose rings were shown to be quasi-free for GE2 in [2] were the non-Euclidean imaginary quadratic fields. In fact that leaves the application of Th. 9.3 of [2] to the ring of Gaussian integers unjustified (I am indebted to J.-P. Serre for drawing this oversight to my attention). In order to justify this application one would have to show either (a) that the Gaussian integers are quasi-free for GE2., or (b) that Th. 9.3 of [2] holds under weaker hypotheses which are satisfied by the Gaussian integers. Our object in this note is to establish (b)–indeed our only course, since the Gaussian integers turn out to be not quasi-free.
as x ranges over R; the structure of E2(R)a has been described in a recent theorem [2; Th. 9.3] for certain rings R, the “quasi-free rings for GE2” (cf. §2 below). Now over a commutative Euclidean domain, E2(R) is just the special linear group SL2(R); this suggests applying the theorem to the ring of integers in a Euclidean number field. However, the only number fields whose rings were shown to be quasi-free for GE2 in [2] were the non-Euclidean imaginary quadratic fields. In fact that leaves the application of Th. 9.3 of [2] to the ring of Gaussian integers unjustified (I am indebted to J.-P. Serre for drawing this oversight to my attention). In order to justify this application one would have to show either (a) that the Gaussian integers are quasi-free for GE2., or (b) that Th. 9.3 of [2] holds under weaker hypotheses which are satisfied by the Gaussian integers. Our object in this note is to establish (b)–indeed our only course, since the Gaussian integers turn out to be not quasi-free.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1968
References
- 27
- Cited by

