Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Basu, Saugata
Pollack, Richard
and
Roy, Marie-Françoise
1996.
On the combinatorial and algebraic complexity of quantifier elimination.
Journal of the ACM,
Vol. 43,
Issue. 6,
p.
1002.
Basu, Saugata
Pollack, Richard
and
Roy, Marie-Françoise
1997.
On Computing a Set of Points Meeting Every Cell Defined by a Family of Polynomials on a Variety.
Journal of Complexity,
Vol. 13,
Issue. 1,
p.
28.
MatouŠek, Jiří
1998.
European Congress of Mathematics.
Vol. 169,
Issue. ,
p.
1.
Zell, Thierry
1999.
Betti numbers of semi-Pfaffian sets.
Journal of Pure and Applied Algebra,
Vol. 139,
Issue. 1-3,
p.
323.
Agarwal, Pankaj K.
and
Sharir, Micha
2000.
Handbook of Computational Geometry.
p.
49.
Rónyai, Lajos
Babai, László
and
Ganapathy, Murali
2001.
On the number of zero-patterns of a sequence of polynomials.
Journal of the American Mathematical Society,
Vol. 14,
Issue. 3,
p.
717.
Basu, Saugata
2001.
Different bounds on the different Betti numbers of semi-algebraic sets.
p.
288.
Basu, Saugata
Pollack, Richard
and
Roy, Marie-Francoise
2003.
Algorithms in Real Algebraic Geometry.
Vol. 10,
Issue. ,
p.
201.
Roy, Marie-Françoise
2003.
Discrete and Computational Geometry.
Vol. 25,
Issue. ,
p.
737.
Basu, Saugata
Pollack, Richard
and
Roy, Marie-Françoise
2004.
On the Betti numbers of sign conditions.
Proceedings of the American Mathematical Society,
Vol. 133,
Issue. 4,
p.
965.
Mosig, Axel
and
Clausen, Michael
2005.
Approximately matching polygonal curves with respect to the Fréchet distance.
Computational Geometry,
Vol. 30,
Issue. 2,
p.
113.
2006.
Algorithms in Real Algebraic Geometry.
Vol. 10,
Issue. ,
p.
237.
Basu, Saugata
Pollack, Richard
and
Roy, Marie-Françoise
2009.
An asymptotically tight bound on the number of semi-algebraically connected components of realizable sign conditions.
Combinatorica,
Vol. 29,
Issue. 5,
p.
523.
Solymosi, József
and
Tao, Terence
2012.
An Incidence Theorem in Higher Dimensions.
Discrete & Computational Geometry,
Vol. 48,
Issue. 2,
p.
255.
KAPLAN, HAIM
MATOUŠEK, JIŘÍ
SAFERNOVÁ, ZUZANA
and
SHARIR, MICHA
2012.
Unit Distances in Three Dimensions.
Combinatorics, Probability and Computing,
Vol. 21,
Issue. 4,
p.
597.
Cheng, Siu-Wing
and
Lam, Chi-Kit
2013.
Shape matching under rigid motion.
Computational Geometry,
Vol. 46,
Issue. 6,
p.
591.
Agarwal, Pankaj K.
Matoušek, Jiří
and
Sharir, Micha
2013.
On Range Searching with Semialgebraic Sets. II.
SIAM Journal on Computing,
Vol. 42,
Issue. 6,
p.
2039.
Basu, Saugata
2015.
A Complexity Theory of Constructible Functions and Sheaves.
Foundations of Computational Mathematics,
Vol. 15,
Issue. 1,
p.
199.
Aschenbrenner, Matthias
Dolich, Alf
Haskell, Deirdre
Macpherson, Dugald
and
Starchenko, Sergei
2015.
Vapnik-Chervonenkis density in some theories without the independence property, I.
Transactions of the American Mathematical Society,
Vol. 368,
Issue. 8,
p.
5889.
Deutsch, Alin
Li, Yuliang
and
Vianu, Victor
2016.
Verification of Hierarchical Artifact Systems.
p.
179.

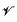 a variety of real dimension
a variety of real dimension 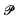 = {
= {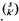 (
(