Article contents
On the frequency distribution of partial quotients of U-numbers
Published online by Cambridge University Press: 26 February 2010
Extract
In Mahler's classification of complex numbers [10] (see [4]), a transcendental number ξ is called a U-number if there exists a fixed integer N ≥ 1 so that for all ω > 0, there exists a polynomial 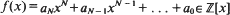 so that
so that
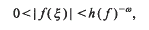
where the height h(f) = max {|α0|, |α1|, …, |αN|}. The number ξ is called a Um-number if the above holds for N = m but for no smaller value of N (examples and further details may be found in [9,1 and 2]). Thus the set of U1-numbers is precisely the set of Liouville numbers. In this paper we investigate the statistical behavior of the partial quotients of real U-numbers, in particular, U2-numbers. In addition, we demonstrate the existence of a U2-number with the property that if it is translated by any nonnegative integer and then squared, the result is a Liouville number. Related results involving badly approximate U2-numbers are also discussed.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1993
References
- 1
- Cited by

