No CrossRef data available.
Article contents
On the asymptotic properties of linear differential equations
Part of:
Qualitative theory
Published online by Cambridge University Press: 26 February 2010
Extract
We consider the second order linear differential equation
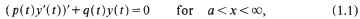
where p and q are real-valued members of 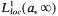 with p(t)>0 for t ∈ [α, ∞). In particular we consider the following three questions dealing with the asymptotic behavior of solutions of (1.1).
with p(t)>0 for t ∈ [α, ∞). In particular we consider the following three questions dealing with the asymptotic behavior of solutions of (1.1).
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1987
References
1.Atkinson, F. V.. On second order linear oscillations. Rev. Mat. Fis. Teor (Turcoman), Ser. A, 8 (1951), 71–87.Google Scholar
2.Atkinson, F. V.. Asymptotic formulae for linear oscillations. Proc. Glasgow Math. Assoc., 3 (1957), 105–111.Google Scholar
3.Cassell, J. S.. An extension of the Liouville Green asymptotic formula for oscillatory second order differential equations. Proc. Royal Soc. Edinburgh, 100 A (1985), 180–190.CrossRefGoogle Scholar
4.Cassel, J. S.. Generalized Liouville Green asymptotic approximation for second order differential equations. Proc. Royal Soc. Edinburgh, 103A (1986), 229–239.CrossRefGoogle Scholar
6.Harris, B. J.. On the zeros of solutions of differential equations. J. London Math. Soc. (2), 27 (1983), 447–464.Google Scholar
7.Harris, B. J.. Limit circle criteria for second order differential expressions. Quart. J. Math. Oxford (2), 35 (1984), 415–427.CrossRefGoogle Scholar
8.Harris, B. J.. On the oscillation of solutions of linear differential equations. Mathematika, 31 (1984), 214–226.CrossRefGoogle Scholar

