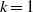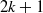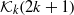Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bagchi, Bhaskar
and
Datta, Basudeb
2014.
On stellated spheres and a tightness criterion for combinatorial manifolds.
European Journal of Combinatorics,
Vol. 36,
Issue. ,
p.
294.
Burton, Benjamin A.
Datta, Basudeb
Singh, Nitin
and
Spreer, Jonathan
2015.
Separation index of graphs and stacked 2-spheres.
Journal of Combinatorial Theory, Series A,
Vol. 136,
Issue. ,
p.
184.
Bagchi, Bhaskar
2015.
A tightness criterion for homology manifolds with or without boundary.
European Journal of Combinatorics,
Vol. 46,
Issue. ,
p.
10.
Cavicchioli, Alberto
and
Spaggiari, Fulvia
2021.
On reduced complexity of closed piecewise linear 5-manifolds.
Periodica Mathematica Hungarica,
Vol. 83,
Issue. 2,
p.
144.