Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wittmann, Christian
2004.
𝑝-class groups of certain extensions of degree 𝑝.
Mathematics of Computation,
Vol. 74,
Issue. 250,
p.
937.
GRAS, GEORGES
2017.
Invariant generalized ideal classes – structure theorems for p-class groups in p-extensions.
Proceedings - Mathematical Sciences,
Vol. 127,
Issue. 1,
p.
1.

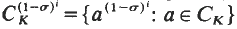 for
for 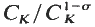 is an elementary abelian
is an elementary abelian 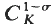 . We let
. We let