Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bugeaud, Yann
2015.
Around the Littlewood conjecture in Diophantine approximation.
Publications mathématiques de Besançon. Algèbre et théorie des nombres,
p.
5.
Badziahin, Dzmitry
2016.
Computation of the Infimum in the Littlewood Conjecture.
Experimental Mathematics,
Vol. 25,
Issue. 1,
p.
100.
Badziahin, Dzmitry
and
Harrap, Stephen
2017.
Cantor-winning sets and their applications.
Advances in Mathematics,
Vol. 318,
Issue. ,
p.
627.
Widmer, Martin
2017.
Asymptotic diophantine approximation: the multiplicative case.
The Ramanujan Journal,
Vol. 43,
Issue. 1,
p.
83.
Dick, Josef
Pillichshammer, Friedrich
Suzuki, Kosuke
Ullrich, Mario
and
Yoshiki, Takehito
2018.
Lattice-based integration algorithms: Kronecker sequences and rank-1 lattices.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 197,
Issue. 1,
p.
109.
LIU, WENCAI
2019.
SOME REFINED RESULTS ON THE MIXED LITTLEWOOD CONJECTURE FOR PSEUDO-ABSOLUTE VALUES.
Journal of the Australian Mathematical Society,
Vol. 107,
Issue. 1,
p.
91.
FREGOLI, REYNOLD
2022.
Multiplicatively badly approximable matrices up to logarithmic factors.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 172,
Issue. 3,
p.
685.
Beresnevich, Victor
Nesharim, Erez
and
Yang, Lei
2022.
Winning property of badly approximable points on curves.
Duke Mathematical Journal,
Vol. 171,
Issue. 14,
Badziahin, Dzmitry
and
Bugeaud, Yann
2022.
Multiplicative p-Adic Approximation.
Michigan Mathematical Journal,
Vol. 71,
Issue. 1,
Chow, Sam
and
Technau, Niclas
2024.
Littlewood and Duffin–Schaeffer-Type Problems in Diophantine Approximation.
Memoirs of the American Mathematical Society,
Vol. 296,
Issue. 1475,
Fregoli, Reynold
and
Kleinbock, Dmitry
2026.
On multiplicatively badly approximable vectors.
Journal of Number Theory,
Vol. 278,
Issue. ,
p.
570.

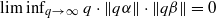 for all (
for all (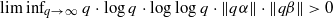 is of full dimension.
is of full dimension.