No CrossRef data available.
Article contents
Note on difference-covers that are not k-sum-covers
Part of:
Designs and configurations
Published online by Cambridge University Press: 26 February 2010
Extract
For some integer modulus q let F be a subset of Z(q), the additive group of residues modulo q. As in «1» we shall write
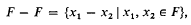
and
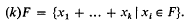
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1974
References
1.Jackson, T. H., Williamson, J. H. and Woodall, D. R.. “Difference-covers that are not k-sum covers. I”, Proc. Camb. Phil. Soc, 72 (1972), 425–438.CrossRefGoogle ScholarPubMed
2.Jackson, T. H.. “Asymmetric sets of residues”, Mathematika, 19 (1972), 191–199.CrossRefGoogle Scholar
3.Connolly, D.. “Integer difference covers which are not k-sum covers, for k = 6, 7”, Proc. Camb. Phil. Soc, 74 (1973), 17–28.CrossRefGoogle Scholar
4.Haight, J. A.. “Difference covers which have small k-sums for any k”, Mathematika, 20 (1973), 109–118.CrossRefGoogle Scholar

