Article contents
Lattice covering of space with symmetric convex bodies
Published online by Cambridge University Press: 26 February 2010
Abstract
In 1959 C. A. Rogers gave the following estimate for the density ϑ(k) of lattice-coverings of euclidean d-space Ed with convex bodies 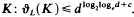 . Here, c is a suitable constant which does not depend on d and K. Moreover, Rogers proved that for the unit ball Bd the upper bound can be replaced by
. Here, c is a suitable constant which does not depend on d and K. Moreover, Rogers proved that for the unit ball Bd the upper bound can be replaced by 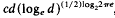 , which is, of course a major improvement. In the present paper we show that such an improvement can be obtained for a larger class of convex bodies. In particular, we prove the following theorem. Let K be a convex body in Ed, and let k be an integer satisfying k > log2 loge d + 4. If there exist at least k hyperplanes H1,…, Hk with normals mutually perpendicular and an affine transformation A such that A(K) is symmetrical with respect to Hl,…,Hk, respectively, then
, which is, of course a major improvement. In the present paper we show that such an improvement can be obtained for a larger class of convex bodies. In particular, we prove the following theorem. Let K be a convex body in Ed, and let k be an integer satisfying k > log2 loge d + 4. If there exist at least k hyperplanes H1,…, Hk with normals mutually perpendicular and an affine transformation A such that A(K) is symmetrical with respect to Hl,…,Hk, respectively, then 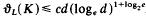 . Actually, for a bound of this type we do not even need any symmetry assumption. In fact, some weaker properties concerning shadow boundaries will suffice.
. Actually, for a bound of this type we do not even need any symmetry assumption. In fact, some weaker properties concerning shadow boundaries will suffice.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1985
References
- 8
- Cited by

