Article contents
THE JUMPING CHAMPION CONJECTURE
Published online by Cambridge University Press: 04 May 2015
Abstract
An integer 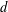 $d$ is called a jumping champion for a given
$d$ is called a jumping champion for a given  $x$ if
$x$ if 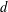 $d$ is the most common gap between consecutive primes up to
$d$ is the most common gap between consecutive primes up to  $x$. Occasionally, several gaps are equally common. Hence, there can be more than one jumping champion for the same
$x$. Occasionally, several gaps are equally common. Hence, there can be more than one jumping champion for the same  $x$. In 1999, Odlyzko et al provided convincing heuristics and empirical evidence for the truth of the hypothesis that the jumping champions greater than 1 are 4 and the primorials
$x$. In 1999, Odlyzko et al provided convincing heuristics and empirical evidence for the truth of the hypothesis that the jumping champions greater than 1 are 4 and the primorials 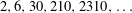 $2,6,30,210,2310,\ldots \,$. In this paper, we prove that an appropriate form of the Hardy–Littlewood prime
$2,6,30,210,2310,\ldots \,$. In this paper, we prove that an appropriate form of the Hardy–Littlewood prime 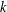 $k$-tuple conjecture for prime pairs and prime triples implies that all sufficiently large jumping champions are primorials and that all sufficiently large primorials are jumping champions over a long range of
$k$-tuple conjecture for prime pairs and prime triples implies that all sufficiently large jumping champions are primorials and that all sufficiently large primorials are jumping champions over a long range of  $x$.
$x$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2015
References
- 5
- Cited by

