No CrossRef data available.
Article contents
INTRINSIC DIOPHANTINE APPROXIMATION ON GENERAL POLYNOMIAL SURFACES
Published online by Cambridge University Press: 02 November 2016
Abstract
We study the Hausdorff measure and dimension of the set of intrinsically simultaneously 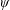 $\unicode[STIX]{x1D713}$ -approximable points on a curve, surface, etc, given as a graph of integer polynomials. We obtain complete answers to these questions for algebraically “nice” manifolds. This generalizes earlier work done in the case of curves.
$\unicode[STIX]{x1D713}$ -approximable points on a curve, surface, etc, given as a graph of integer polynomials. We obtain complete answers to these questions for algebraically “nice” manifolds. This generalizes earlier work done in the case of curves.
MSC classification
Primary:
11J83: Metric theory
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
Beresnevich, V., Rational points near manifolds and metric Diophantine approximation. Ann. of Math. (2)
175(1) 2012, 187–235.Google Scholar
Beresnevich, V., Dickinson, D. and Velani, S., Measure theoretic laws for lim sup sets. Mem. Amer. Math. Soc.
179(846) 2006, 1–91.Google Scholar
Beresnevich, V. and Velani, S., A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2)
164(3) 2006, 971–992.Google Scholar
Bernik, V. I. and Dodson, M. M., Metric Diophantine Approximation on Manifolds
(Cambridge Tracts in Mathematics 137
), Cambridge University Press (Cambridge, 1999).Google Scholar
Budarina, N., Dickinson, D. and Levesley, J., Simultaneous Diophantine approximation on polynomial curves. Mathematika
56(1) 2010, 77–85.Google Scholar
Dickinson, H. and Dodson, M. M., Simultaneous Diophantine approximation on the circle and Hausdorff dimension. Math. Proc. Cambridge Philos. Soc.
130(3) 2001, 515–522.Google Scholar
Falconer, K., Fractal Geometry
(Mathematical Foundations and Applications), 3rd edn., John Wiley (Chichester, 2014).Google Scholar
Fishman, L., Kleinbock, D., Merrill, K. and Simmons, D., Intrinsic Diophantine approximation on quadric hypersurfaces. Preprint, 2015, arXiv:1405.7650.Google Scholar
Fishman, L., Kleinbock, D., Merrill, K. and Simmons, D., Intrinsic Diophantine approximation on manifolds: general theory. Preprint, 2015, arXiv:1509.05439.Google Scholar
Ghosh, A., Gorodnik, A. and Nevo, A., Metric Diophantine approximation on homogeneous varieties. Compositio Math.
150(8) 2014, 1435–1456.Google Scholar
Hindry, M. and Silverman, J. H., Diophantine Geometry: An Introduction
(Graduate Texts in Mathematics 201
), Springer (New York, 2000).CrossRefGoogle Scholar
Kleinbock, D. Y. and Margulis, G. A., Flows on homogeneous spaces and Diophantine approximation on manifolds. Ann. of Math. (2)
148(1) 1998, 339–360.Google Scholar
Kleinbock, D. and Merrill, K., Rational approximation on spheres. Israel J. Math.
209
2015, 293–322, doi:10.1007/s11856-015-1219-z.Google Scholar
Schleischitz, J., Rational approximation to surfaces defined by polynomials in one variable. Preprint, 2016, arXiv:1601.02810.Google Scholar

