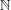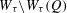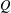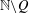Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhao, Cao
and
Chen, Ercai
2018.
Quantitative Recurrence Properties for Systems with Non-uniform Structure.
Taiwanese Journal of Mathematics,
Vol. 22,
Issue. 1,
Zhao, Cao
2021.
Quantitative recurrence properties in the historic set for symbolic systems.
Dynamical Systems,
Vol. 36,
Issue. 2,
p.
181.