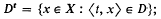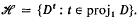Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dellacherie, C.
1975.
Séminaire de Probabilités IX Université de Strasbourg.
Vol. 465,
Issue. ,
p.
336.
1976.
SET THEORY - WITH AN INTRODUCTION TO DESCRIPTIVE SET THEORY.
Vol. 86,
Issue. ,
p.
476.
Wieacker, J. A.
1988.
The convex hull of a typical compact set.
Mathematische Annalen,
Vol. 282,
Issue. 4,
p.
637.
Gruber, Peter M.
1989.
Dimension and structure of typical compact sets, continua and curves.
Monatshefte f�r Mathematik,
Vol. 108,
Issue. 2-3,
p.
149.
GRUBER, Peter M.
1993.
Handbook of Convex Geometry.
p.
1327.
Gartside, Paul M.
and
Lo, Joseph T.H.
2002.
The hierarchy of Borel universal sets.
Topology and its Applications,
Vol. 119,
Issue. 2,
p.
117.
Bloch, W.L.
2003.
Typical elements and meager spaces.
Topology and its Applications,
Vol. 131,
Issue. 1,
p.
39.
Gartside, Paul M.
and
Lo, Joseph T.H.
2003.
Open universal sets.
Topology and its Applications,
Vol. 129,
Issue. 1,
p.
89.
Bloch, W.L.
2007.
Fractal boundaries are not typical.
Topology and its Applications,
Vol. 154,
Issue. 3,
p.
533.

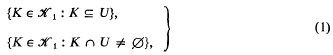
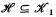 we shall be concerned with sets in [0, 1] ×
we shall be concerned with sets in [0, 1] ×